Factorización LU (Lower-Upper)

La factorización LU o eliminación gaussiana consiste en factorizar una matriz cuadrada en dos matrices triangulares (una matriz triangular superior y una matriz triangular inferior), de modo que el producto de estas dos matrices da la matriz original.

El LU en el término viene del inglés Lower-Upper, que se traduce como inferior-superior.

¿Qué es la factorización LU?

Si tenemos una matriz A, vemos:

L y U son matrices inferiores y superiores triangulares, respectivamente.

Si pensamos en una matriz cuadrada:

Si la matriz A es invertible, es decir, tiene inversa, las matrices L y U son únicas.

¿Qué utilidad tiene la factorización LU?

Este tipo de factorización se puede utilizar para cosas como:

• Resolver sistemas de ecuaciones.
• Cálculo de la matriz inversa: A^-1 = U^-1 L^-1

Un ejemplo

Veamos un ejemplo de factorización LU para entender un poco más este concepto por medio de ejercicios factorizacion lu.

Con la siguiente matriz C, realizamos la factorización LU:

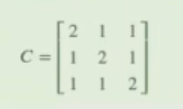
Aquí vamos a usar scipy para hacerlo. Para ello, lo único que tenemos que hacer es emplear el módulo de álgebra lineal de scipy y añadir lu al final, que es lo que hace la factorización.

Entonces, esto nos va a devolver la matriz l y la matriz u.

En Python, importamos el módulo NumPy y lo veríamos así:

//factorización lu de una matriz 4x4
import numpy as np
from scipy import linalg

C = np.array([[2, 1, 1],
              [1, 2, 1],
              [1, 1, 2]])

_, l, u = linalg.lu(C)

l

array (

[[1. , 0. , 0. ],

[0.5 , 1. , 0. ],

[0.5 , 0.33333333 , 1. ],])

u

array (

[[2. , 1. , 1. ],

[0. , 1.5 , 0.5 ],

[0. , 0. , 1.33333333],])

Ambas son matrices triangulares.

Podemos comprobar que la fórmula de factorización LU es correcta y que al multiplicar lxu nos da la matriz original. Esto se logra realizando el producto matricial de L y U:

print (C)

([[2, 1, 1],

[1, 2, 1],

[1, 1, 2]])

En este caso, estamos viendo la factorización LU o lower upper, que nos brinda la posibilidad de resolver diversos problemas relacionados con matrices.

Descomponer un sistema de ecuaciones utilizando factorización LU

Veamos cómo hacer descomposicion de matrices:

1. Obtener las matrices triangulares, esto es, la matriz triangular inferior L y la matriz triangular superior U.
2. Resolver Ly = B (para encontrar y).
3. El resultado del paso anterior se guarda en una matriz nueva de nombre y.
4. Realizar Ux = y (para encontrar x).
5. El resultado del paso anterior se almacena en una matriz nueva llamada x, la cual da los valores correspeondientes a las incógnitas de la ecuación.

Vamos a encontrar las soluciones del sistema (usando la factorización LU):

Este sistema puede escribirse como:

Donde:

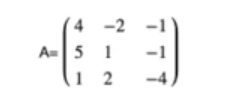
Y B es igual a:

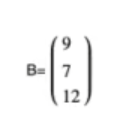
Primero calculamos las matrices L y U:

#factorización LU
A = np.array ([[4,  -2,  -1],
                         [5,  1,  -1],
                         [1,  2,  -4]])

_, L, U = linalg.lu (A)

print (L)
print (U)

[[1. 0. 0. ]

[0.8 1. 0. ]

[0.2 -0.64285714 1. ]]

[[5. 1. -1. ]

[0. -2.8 -0.2 ]

[0. -0. -3.92857143]]

El siguiente paso es resolver Ly = B y guardarlo en la variable y:

#factorización LU
import sympy as sp
import numpy as np

B = np.array ([[9],
                         [7],
                         [12]])

L:B = np.append (L, B, axis = 1)
print (L_B)

[[1. 0. 0. 9. ]

[0.8 1. 0. 7. ]

[0.2 -0.64285714 1. 12. ]]

Ahora resolvemos este sistema lineal:

#factorización LU
from sympy import MAtrix, solve_linear_system
from sympy.abc import x, y, z

L_B = Matrix (L_B)

y = solve_linear_system (L_B,   x,   y,   z)
print (y)

{x: 9.00000000000000, y: -0.200000000000000, z: 10.0714285714286}

Luego, resolvemos Ux = y y lo guardamos en la variable x:

#factorización LU
y_res = list (y.values ())
y_array = np.array ((y_res))
print (y_array)
print (y_array.shape)

#Reshape y_array to (3, 1)
y_reshape = y_array.reshape (3, 1)

y = Matrix (y_reshape)
U_y = np.append (U, y, axis = 1)
print (U_y)

[[9.00000000000000 -0.200000000000000 10.0714285714286]]

(1, 3)

[[5.0 1.0 -1.0 9.0000000000000]

[0.0 -2.8 -0.19999999999999996 -0.20000000000000]

[0.0 0.0 -3.9285714285714384 10.0714285714586]]

print (U_Y.shape)

(3, 4)

Por último, resolvemos dicho sistema:

#factorización LU
from sympy.abc import x, y, z

x = solve_linear_system (Matrix (U_Y), x  y,  z)
print (X)

{x: 1.23636363636364, y: 0.254545454545455, z: -2:56363636363636}

Ahora que has aprendido todo lo necesario sobre la factorización LU, puedes seguir formándote en el mundo del Big Data para convertirte en un experto en el sector. Para acceder a una de las disciplinas más demandadas y con mejores salarios del mundo laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra e intensiva en la que adquirirás, en cuestión de meses, todos los conocimientos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y da el paso que cambiará tu futuro!