Figuras geométricas y fractales con Matplotlib

¿Sabías que se pueden dibujar figuras geométricas y fractales con Matplotlib? En este artículo te enseñaremos cómo crear algunas de ellas gracias a esta librería, la cual tiene muchísimas utilidades, entre ellas, la que te presentaremos a continuación.

Figuras geométricas y fractales con Matplotlib

Figuras planas

Vamos a dibujar un círculo centrado en el (0, 0) con radio de 1.0.

#Figuras geométricas y fractales con Matplotlib
import matplotlib.pyplot as plt

#Vamos a separar la creación del círculo y el mostrar la figura en dos funciones
def crear_circulo ():
       circulo = plt.Circle ((0, 0), radius = 1.0)
       return circulo
#Con esta función creamos un círculo centrado en (0,0) con radio de 1
#Lo que devuelve es el círculo creado

#Creamos ahora la función para mostrar la figura con método genérico
def mostrar_figura (patch):
       #Para devolver los ejes actuales
       ax = plt.gca ()
       #Le agregamos la figura que le pasamos usando la función mostrar_figura
       ax.add_patch (patch)
       #Los límites de los ejes
       plt.axis ('scaled')
       #Mostramos la figura
       plt.show ()

c = crear_círculo ()
mostrar_figura (c)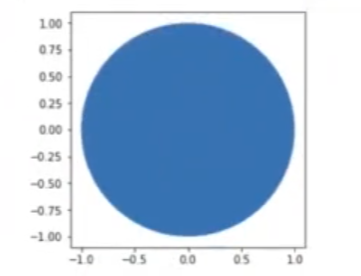

Ahora procedamos a dibujar una elipse de 0.1 de ancho y 0.4 de alto.

#Figuras geométricas y fractales con Matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse

def crear_elipse ():
       elipse = Ellipse ((0, 0), width = 0.1, height = 0.4)
       return elipse

def mostrar_figura (patch):     
       ax = plt.gca ()
       ax.add_patch (patch)
       plt.axis ('scaled')
       plt.show ()

c = crear_elipse ()
mostrar_figura (c)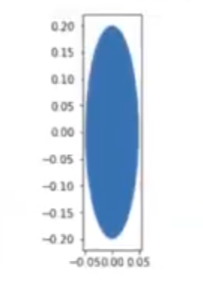

Así pues, tenemos una figura que es mucho más achatada que la anterior.

Ahora, lo que haremos será dibujar una elipse de 0.1 de ancho y 0.4 de alto con un giro de 90°.

#Figuras geométricas y fractales con Matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse

def crear_elipse ():
       elipse = Ellipse ((0, 0), width = 0.1, height = 0.4, angle = 90)
       return elipse
def mostrar_figura (patch):
       ax = plt.gca ()
       ax.add_patch (patch)
       plt.axis ('scaled') 
       plt.show ()

c = crear_elipse ()
mostrar_figura (c)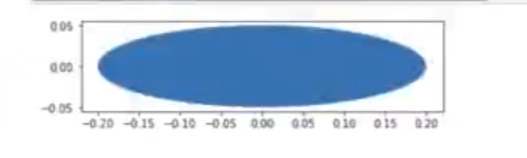

Ahora tenemos un caso contrario al anterior, en donde hemos alargado la figura, pero de manera horizontal, mientras que en el otro caso la alargamos de modo vertical.

Fractales

Los fractales son patrones geométricos complejos o formas que surgen de fórmulas matemáticas sorprendentemente simples.

En comparación con las formas geométricas, como los círculos y los rectángulos, un fractal parece irregular y sin ningún patrón o descripción obvios, pero si se observa detenidamente, veremos que los patrones emergen y la forma completa está compuesta de numerosas copias de sí misma.

Debido a que los fractales implican la aplicación repetitiva de la misma transformación geométrica de puntos, los programas de ordenador son adecuados para crearlos.

Los fractales abundan en la naturaleza: los ejemplos populares incluyen árboles y copos de nieve.

Transformaciones de puntos en el plano

Una idea básica en la creación de fractales es la de la transformación de un punto.

Dado un punto,P (x, y), un ejemplo de una transformación es (x, y) → (x + 1, y + 1).

Esta transformación es, por lo tanto, una regla que describe cómo se mueve un punto en el plano XY, comenzando desde una posición inicial y moviéndose a un punto diferente en cada iteración.

Pensemos ahora que, en lugar de una regla de transformación, hay dos reglas de este tipo y una de estas transformaciones se selecciona al azar en cada paso. Consideremos estas reglas:

1. Regla 1: (x, y) → (x + 1, y + 1)
2. Regla 2: (x, y) → (x + 1, y + 1)

Si tenemos el punto (1, 1), podríamos tener, por ejemplo, la siguiente secuencia:

• P1 (1, 1) → P2 (2, 0) (Regla 1)
• P2 (2, 0) → P3 (3, 1) (Regla 2)
• P3 (3, 1) → P4 (4, 2) (Regla 2)
• P4 (4, 2) → P5 (5, 1) (Regla 1)
• etc.

La regla de transformación se elige al azar, teniendo cada regla una probabilidad igual de ser seleccionada.

No importa cuál se elija, los puntos avanzarán hacia la derecha porque aumentamos la coordenada x en ambos casos. A medida que los puntos van hacia la derecha, se mueven hacia arriba o hacia abajo, creando así una ruta en zigzag.

Gracias a estos ejercicios en Python, hemos visto cómo funcionan las figuras geométricas y fractales con Matplotlib, por lo que es el momento de seguir aprendiendo sobre Big Data. Si quieres acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral, no te pierdas el Full Stack Bootcamp Data Science, una formación intensiva e íntegra en la que adquirirás, en escasos meses, todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a transformar tu futuro!