¿Sabes interpretar la fórmula matemática del producto escalar? El producto escalar o producto interno es el resultante de la multiplicación de dos vectores. Lo que hacemos con este es multiplicar los componentes y el resultado que nos dé es el producto escalar.
Fórmula matemática del producto escalar
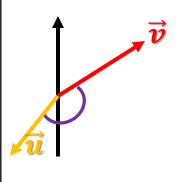
Tenemos este gráfico:
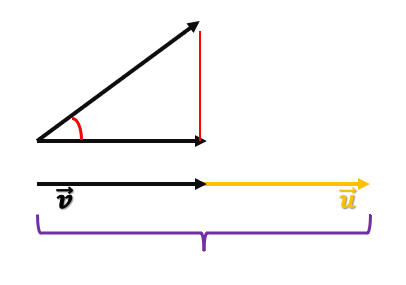
Veamos la fórmula matemática del producto escalar:
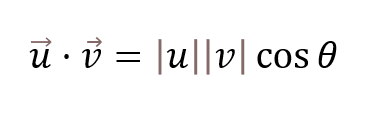
La fórmula matemática del producto escalar viene dada por los componentes de la anterior imagen. Tenemos, pues, el módulo del vector u (|u|), el módulo del vector v (|v|) y el ángulo entre ambos (cos θ).
¿De qué nos sirve esto? Esto es bastante importante, dado que nos da pie a introducir la similitud entre vectores, muy usada en machine learning.
Casos especiales donde es aplicable la fórmula matemática del producto escalar
Primer caso
Tenemos, por lo tanto, el vector v y el vector u. ¿Qué sucede con el producto escalar? ¿Será mayor, menor o igual a cero?
Si utilizamos la ecuación y decimos que tenemos dos vectores que son perpendiculares, ¿qué significa esto? Que el producto escalar será igual a 0.
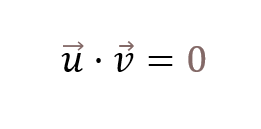
El producto escalar es igual a 0 porque, como son perpendiculares, el coseno del ángulo de 90° es 0.
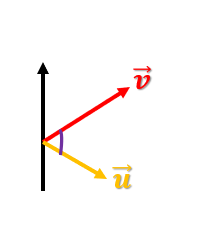
Segundo caso
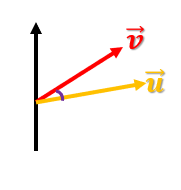
En este segundo caso tenemos dos vectores: el u y el v. En este caso el ángulo es menor a 90°, es decir, ambos vectores no son perpendiculares.
θ < 90°
¿Cuál será el resultado en esta situación? ¿El producto escalar será positivo, negativo…?
Una forma de ver esto es dibujando la ecuación del coseno:
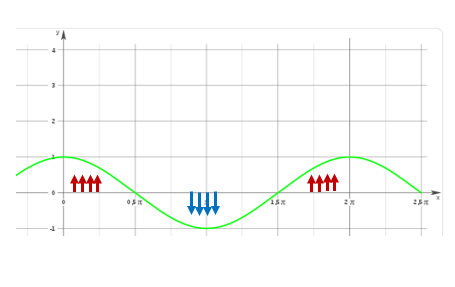
Aquí vemos que hay unas partes positivas (marcadas con flechas rojas) y unas partes negativas (marcadas con azul). Esto sería el coseno de θ.
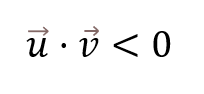
Lo que estamos viendo aquí es que, si el coseno es menor que 90, es positivo; por tanto, el producto escalar también va a ser positivo.
Tercer caso
Este tercer caso es un caso opuesto al anterior, ya que en esta ocasión el ángulo entre el vector v y el vector v es mayor que 90°. Bajo estas condiciones, el producto escalar va a ser negativo. Esto viene dado por la gráfica del coseno, donde podemos ver que, en los números con un ángulo menor que 90°, el producto escalar es positivo. Por el contrario, en ángulos mayores a 90° el producto escalar es negativo.
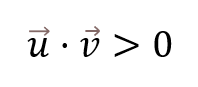
¿Qué sigue?
El Big Data es una de las áreas en las que más trabajos se ofertan. Si te interesa acceder a este tipo de opciones laborales de alta empleabilidad y altos sueldos, échale un vistazo al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos necesarios para triunfar en este mundillo. Con la compañía de los mejores profesionales, tu proceso formativo te catapultará al éxito. ¡Entra e infórmate para alcanzar todas tus metas!











