Forward y back propagation en Deep Learning

Forward y back propagation en Deep Learning son dos de los procesos más importantes en el desarrollo de este campo del manejo de los macrodatos. Por ello, conocer cómo se desarrollan y para qué sirven es de gran relevancia para un buen data scientist.

Por este motivo, en el desarrollo de este post te exponemos cómo funcionan forward y back propagation en Deep Learning, de manera que sepas cómo implementarlos en tu análisis de datos.

Forward y back propagation en Deep Learning

Forward y back propagation en Deep Learning son dos de los procesos más utilizados e importantes en el procesamiento de los macrodatos. Sin embargo, su comprensión se produce en la marcha.

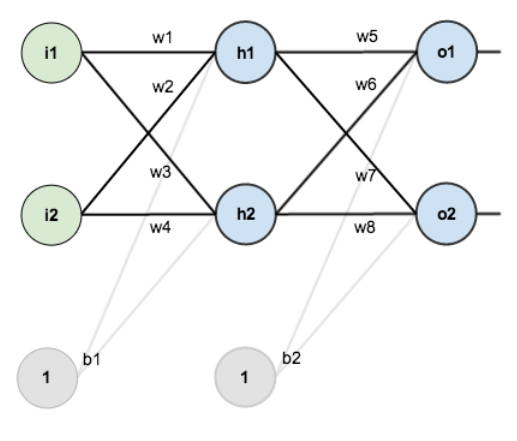
Por ello, vamos a diseñar una red neuronal sencilla que nos permita ejemplificar su entrenamiento. En esta imagen, podemos ver una red con una primera capa de dos neuronas, una capa oculta de dos neuronas y una capa de salida de otras dos neuronas. Además, la capa interna y la de salida tienen también bias.

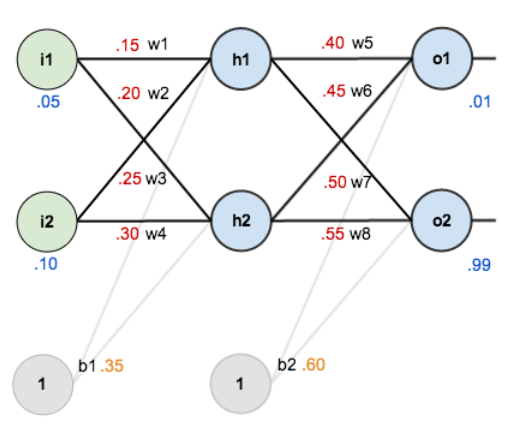
Por simplicidad, vamos a suponer que nuestro training set se compone solo de un elemento: 0.05, 0.1, que es de clase 1 (podría ser de clase 0, si la probabilidad de la neurona o1 es mayor que la de la neurona o2, o de clase 1 si ocurre lo contrario). En la siguiente imagen puedes ver la red con los pesos inicializados aleatoriamente, el elemento del training set a la entrada y la salida deseada:

Ya tenemos nuestra red definida y lista para entrenar. Pero ¿cómo aprende una red?

Mediante el forward y back propagation en Deep Learning.

Forward pass

El feed-forward o pasada hacia delante consiste en calcular la salida de nuestra red con los valores actuales de los pesos. Para ello, siguiendo con nuestro ejemplo, lo que hacemos es alimentar (feed forward) la red con nuestro elemento de entrenamiento.

Pero antes de nada, vamos a ver cómo es realmente una neurona:

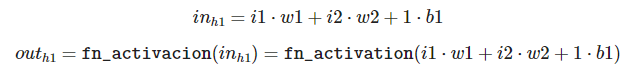
Donde fn_activacion es la función de activación elegida. Aquí puedes visualizar algunas de estas funciones, que luego veremos con más detalle.

Primero, vamos a ver qué necesitamos calcular, por orden. Veamos primero nuestra red y la estructura de la neurona otra vez:

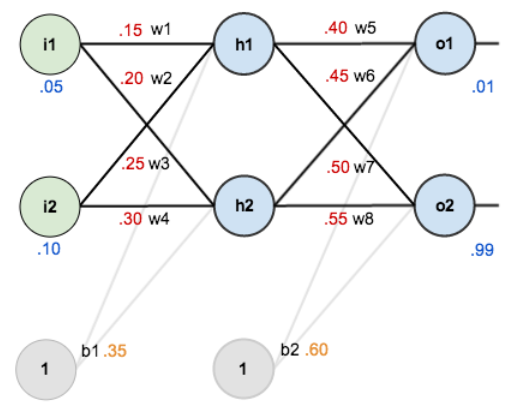
De acuerdo con esto, para calcular o1 y o2 necesitamos:

• Para la primera capa, la oculta:
  • inh1 y outh1
  • inh2 y outh2

• Para la última capa, la de salida:
  • ino1 y outo1
  • ino2 y outo2

Donde o1 = outo1 y o2 = outo2.

Con lo cual, tenemos que calcular:

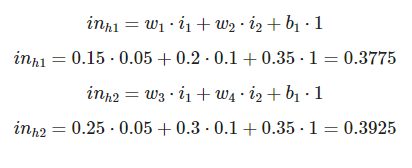
in_h1 = 0.15*0.05+0.2*0.1+0.35*1
print(in_h1)

0.3775

in_h2 = 0.25*0.05+0.3*0.1+0.35*1
print(in_h2)

0.39249999999999996

Ahora, para obtener outh1 y outh2, necesitamos aplicar la fn_activacion. En este caso, hemos escogido la función de activación logística:

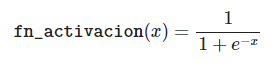
Por lo tanto:

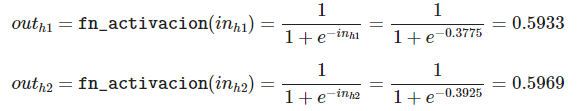
import numpy as np
out_h1 = 1 / (1+np.exp(-in_h1))
print(out_h1)

0.5932699921071872

out_h2 = 1 / (1+np.exp(-in_h2))
print(out_h2)

0.596884378259767

Vamos a ver cómo llevamos el cálculo de nuestra salida:

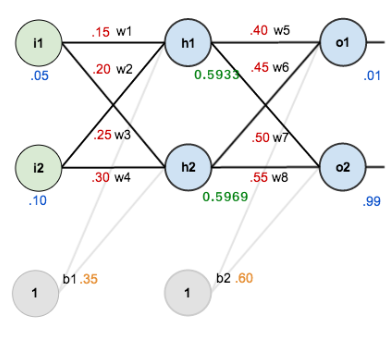
¡Solo nos queda calcular o1 y o2! Vamos allá:

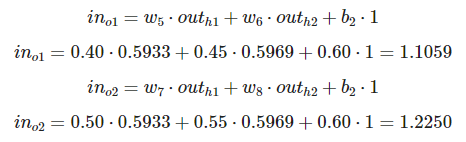
Por lo tanto, aplicando la función de activación:

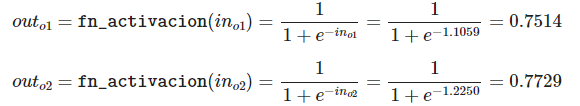
in_o1 = 0.40*0.5933+0.45*0.5969+0.60*1
print(in_o1)

1.105925

in_o2 = 0.50*0.5933+0.55*0.5969+0.60*1
print(in_o2)

1.224945

out_o1 = 1 / (1+np.exp(-in_o1))
print(out_o1)  # target_o1 = 0.01

0.751368625185488

out_o2 = 1 / (1+np.exp(-in_o2))
print(out_o2)  # target_o2 = 0.99

0.7729326066130681
¡Ya tenemos las predicciones de nuestra red neuronal calculadas! Sin embargo, no hemos terminado, porque no se parecen en nada al 0.01 y 0.99 deseados.

Back propagation

¿Cómo podemos actualizar los pesos, cada uno en función de lo que influya en el error total? Debemos calcular cuánto influye un cambio en un determinado peso con respecto al error total y actualizarlo teniendo en cuenta esta relación.

Por ejemplo, ¿sabes cómo calcular cuánto influye un cambio en el peso w5 en el error total? ¡Estamos hablando de derivadas! Podemos entender cada neurona como una función y aplicar la regla de la cadena para llegar desde el error total hasta el peso w5.

Imagina que cada círculo es una función y que cada flecha una multiplicación. Entonces, utilizando la regla de la cadena, podríamos escribir:

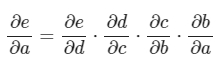
Tras recordar la regla de la cadena, veamos cómo podemos escribir la fórmula que nos indique cúanto cambia el Etotal en función del peso w5:

Continúa aprendiendo más sobre Big Data

En este post, te has familiarizado con forward y back propagation en Deep Learning, sin embargo, te advertimos que aún faltan más procesos por estudiar en este amplio campo del manejo del Big Data.

Por ello, desde KeepCoding, para continuar instruyéndote te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Aquí podrás aprender a desarrollar toda la serie de herramientas, sistemas y lenguajes desarrollados para destacar el valor de los macrodatos. En menos de nueve meses, este proceso te aportará las bases suficientes para convertirte en todo un experto Big Data, gracias a su metodología hands on y de la ayuda de grandes profesionales. ¡Empieza ahora!