La función de enlace es una función que forma parte de los modelos lineales generalizados. Esta relaciona el valor esperado del resultado con los predictores lineales del modelo.
La función de enlace transforma probabilidades de los niveles de una variable de respuesta categórica en una escala continua ilimitada.
Proceso de transformación de la función de enlace
Imaginemos una variable de respuesta binaria que solo puede tener dos valores únicos. Cuando se convierten estos valores a probabilidades, la variable de respuesta pasa de 0 — 1 a −∞ — +∞.
La fórmula para la función de enlace es:
g(μi) = Xi‘β
Donde:
- g(μi) es la función de enlace.
- μi es la respuesta media de la iésima fila.
- Xi es el vector de variables predictoras para la iésima fila.
- β es el vector de coeficientes asociados con los predictores.
Tipos de funciones de enlace
Existen diferentes funciones de enlace, dependiendo de las variables de respuesta que se encuentren:
| Modelos | Tipo de datos | Nombre | Función de enlace |
| Bernoulli | Integer {0, 1} | logit | XΒ = ln(μ / 1 – μ) |
| Binomial | Integer {0, 1, … n} | logit | XΒ = ln(μ / n – μ) |
| Normal distribution | real (-∞, ∞) | identity | XΒ = μ |
| Exponential distribution | real (0, ∞) | negative inverse | XΒ = -μ-1 |
| Gamma distribution | real (0, ∞) | negative inverse | XΒ = -μ-1 |
| Poisson distribution | Integer 0, 1, 2, … | log | XΒ = ln(μ) |
Función de enlace logit
Su forma de uso es:
logitlink(theta, bvalue = NULL, inverse = FALSE, deriv = 0, short = TRUE, tag = FALSE) extlogitlink(theta, min = 0, max = 1, bminvalue = NULL, bmaxvalue = NULL, inverse = FALSE, deriv = 0, short = TRUE, tag = FALSE)Donde:
- theta es un caracter numérico.
- bvalue, bminvalue, bmaxvalue son los valores límite.
La función de enlace logit se utiliza para modelar la probabilidad de éxito como una función de covariables. Su propósito es tomar una combinación lineal de los valores de las covariables y convertir esos valores a la escala de una probabilidad, es decir, entre 0 y 1.
Su fórmula es:
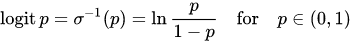
Esta función tiene entre sus propiedades dos destacables:
- Convierte las probabilidades de menos de uno en números negativos, porque el logaritmo de un número entre 0 y 1 siempre debe ser negativo.
- Aplana la curva cuadrada de las probabilidades.
Distribución binomial
La distribución binomial se usa cuando hay exactamente dos resultados mutuamente excluyentes de un ensayo. Estos resultados se etiquetan apropiadamente como éxito y fracaso.
Este tipo de distribución se usa para obtener la probabilidad de observar X éxitos en N pruebas, con la probabilidad de éxito en una sola prueba denotada por p.
La fórmula de esta distribución es:
P (x; p, n) = (nx) (p) x (1 − p) (n − x) for x = 0, 1, 2, ⋯, n
Función de enlace probit
La función de enlace probit es un tipo de regresión donde la variable dependiente tiene apenas dos valores, que pueden ser casi cualquier cosa. Esta función tiene como propósito estimar la probabilidad de que una observación caiga en una categoría, dependiendo de sus características. De ahí su nombre, que está relacionado íntimamente con su objetivo.
Se usa del siguiente modo:
probitlink(theta, bvalue = NULL, inverse = FALSE, deriv = 0, short = TRUE, tag = FALSE)Donde:
- theta es una variable de tipo caracter o numérico.
- bvalue es el valor límite.
La función de enlace probit normalmente se usa para parámetros que se encuentran en el intervalo unitario. Los valores numéricos theta cercanos a 0 o 1 dan como resultado Inf, -Inf, NA o NaN.
Distribución normal
La distribución normal o distribución gaussiana es una distribución de probabilidad que muestra que los datos cercanos a la media son más frecuentes que los datos alejados de la misma.
Tiene una forma de curva de campana.
La fórmula de la distribución normal es:
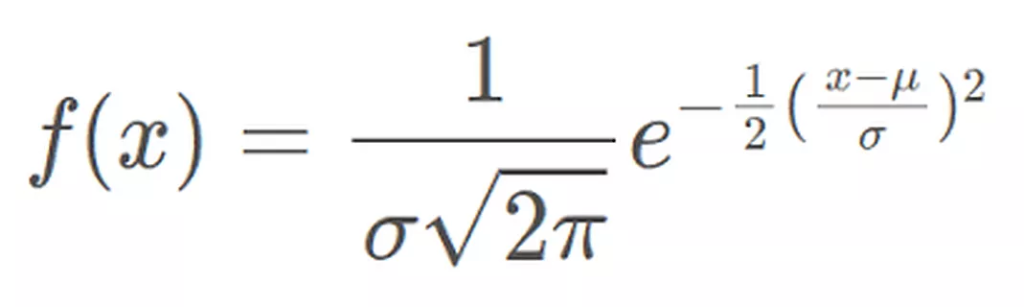
Donde:
- x es el valor de la variable.
- f (x) es la función de probabilidad.
- μ es la media.
- σ es la desviación estándar.
¿Ahora qué sigue?
En este artículo hemos aprendido qué es una función de enlace, cuántas existen y cómo y en qué momento usar cada una de ellas.
Recuerda que si quieres seguir aprendiendo sobre estas temáticas, puedes apuntarte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que en pocos meses podrás adquirir todas las habilidades y conocimientos necesarios para incursionar en el mundo del Big dData, un mercado lleno de oportunidades laborales que impulsarán tu vida. ¡Anímate y solicita más información!



