La función de distribución acumulativa en estadística es una parte fundamental de la cantidad de estrategias que deben aprenderse para un buen conocimiento de estadística. Esto te permite saber si ciertas variables tienen relación o no o si varios grupos de datos se pueden considerar diferentes o iguales.
De hecho, un buen análisis estadístico te aportará, como parte de tu trabajo como data scientist, cauna serie de respuestas que pueden complementar algún modelo posterior que sea mucho más complejo.
Dado a esta importancia, podrás contar con muchas funciones y herramientas que potencien la certeza de los resultados arrojados. Por esto, en este post, te traemos qué es y cómo funciona la función de distribución acumulativa en estadística para el manejo de los macrodatos.
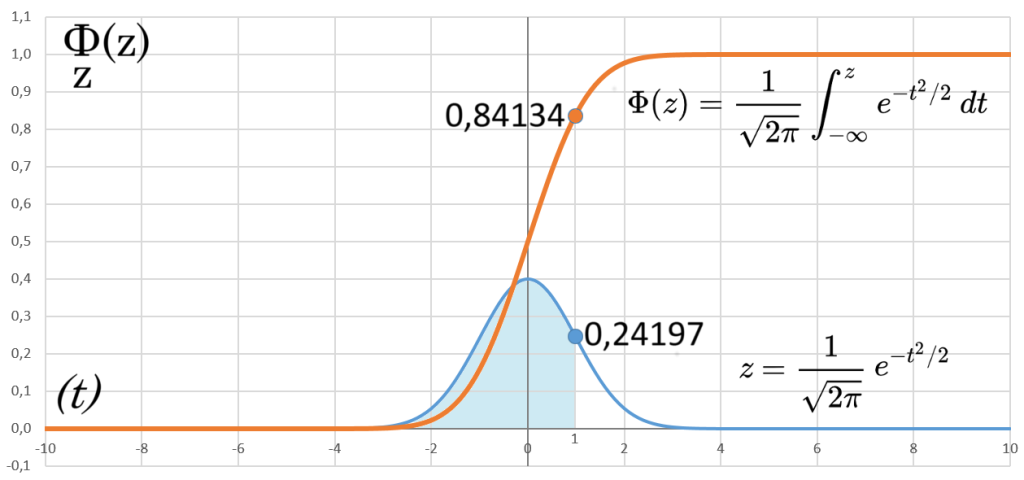
Función de distribución acumulativa en estadística
La función de distribución acumulativa en estadística (o función de distribución acumulada) para el manejo del Big Data te dice la probabilidad de obtener un valor menor o igual a cierto umbral dado en determinada variable aleatoria x.
Por otra parte, si no sabes como se calcula la probabilidad acumulada, debes saber que dicha función se calcula por medio de la siguiente fórmula:
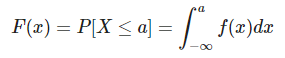
¿Cómo funciona la función de distribución acumulativa en estadística?
Ahora, la mejor forma de comprender qué es la función de distribución acumulada en estadística es a partir de un ejemplo práctico. Entonces, piensa que si eliges una persona al azar en España, ¿cuál sería la probabilidad de que sea menor o igual a los 64 años de edad?
f_poblacion <- poblacion[,c("Total","edad")]
f_poblacion$Ratio <- f_poblacion$Total/sum(f_poblacion$Total)
#densidad acumulada
f_poblacion_subset <- subset(f_poblacion, edad<=64)
paste0("La probabilidad de que eligiendo una persona al azar su edad sea menor o igual a 64 años es ",
round(sum(f_poblacion_subset$Ratio),3)*100,"%")
Así, se calcula que la probabilidad de que eligiendo una persona al azar en España su edad sea menor o igual a los 64 años de edad es del 80.2%.
f_poblacion <- poblacion[,c("Total","edad")]
f_poblacion$Ratio <- f_poblacion$Total/sum(f_poblacion$Total)
plot(cumsum(f_poblacion$Ratio))
#subset(f_poblacion, edad<=64)
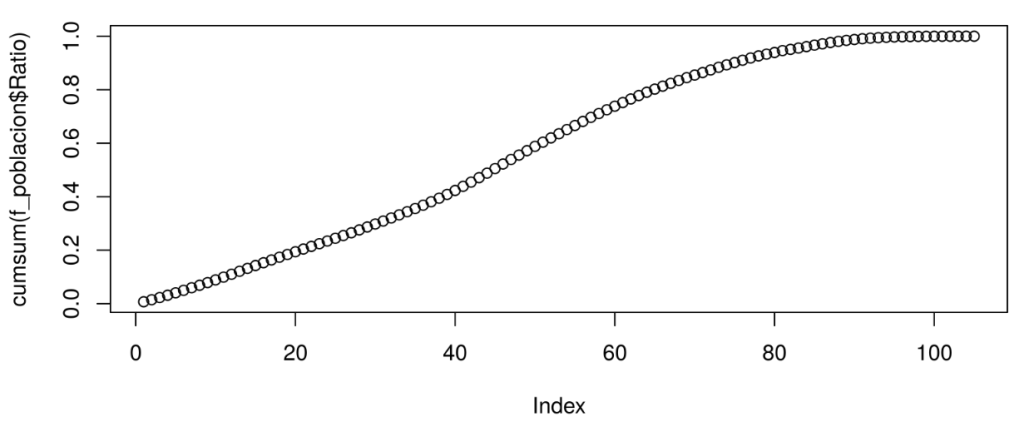
Finalmente, el desarrollo de la gráfica de la función de distribucion acumulativa en estadística para este ejemplo en específico se ilustraría de la siguiente forma:
Aprende más sobre el Big Data y la distribución acumulativa
Ahora que sabes qué es y cómo funciona la función de distribución acumulativa en estadística para el manejo de los macrodatos, esperamos que puedas emplearla en el procesamiento de tus datos. No obstante, debes tener en cuenta que los estadísticos cuentan con muchas más funciones que pueden acoplarse más efectivamente a tu estudio de los macrodatos, de manera que también te aconsejamos continuar aprendiendo sobre el Big Data y sus herramientas.
Si no sabes cómo dar el siguiente paso, desde KeepCoding te ofrecemos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. A través de este, podrás aprender todo lo relacionado con los sistemas, lenguajes y herramientas que más manipulan el Big Data con efectividad y agilidad. En suma, recorrerás tanto de forma teórica como práctica todos y cada uno de los módulos. ¡Solicita información y empieza ahora mismo!







