Podemos utilizar diferentes funciones para optimización en R que, dada una función, nos encuentran el mínimo iterando de forma similar a como hemos visto. Por esto, en este post, te presentamos algunas funciones para optimización en R.
Algunas funciones para optimización en R
Primera función
La primera de estas funciones para optimización en R es una función de una sola dimensión que nos permite calcular el mínimo entre -10 y 10:
In 1: ?optim
In 1: myfunc2 <- function (x) {0.05 * x ^ 2 + sin(x)}
In 1: o <- optimize (myfunc2, interval-c (-10, 10))
o$minimum
-1,42755377906257
$objective
-0,877862826571527
En este caso, el mínimo es -1,42755377906257 y el valor que alcanzamos en ese mínimo es -0,877862826571527.
En la recta, el mínimo sería X y el valor objetivo sería Y.
En este caso, al ser una función de una sola dimensión, nos arroja directamente el mínimo absoluto. No se va a quedar en el mínimo local porque es un intervalo pequeño y explora todo (-10, 10).
In : x <- seq (-10, 10, length.out = 100)
y <- myfunc2(x)
options (repr. plot. height = 4, repr. plot. width = 6)
plot (x, y, t = "l")
points (osminimum, osobjective,co l= "blue")La gráfica de esta función quedaría así:
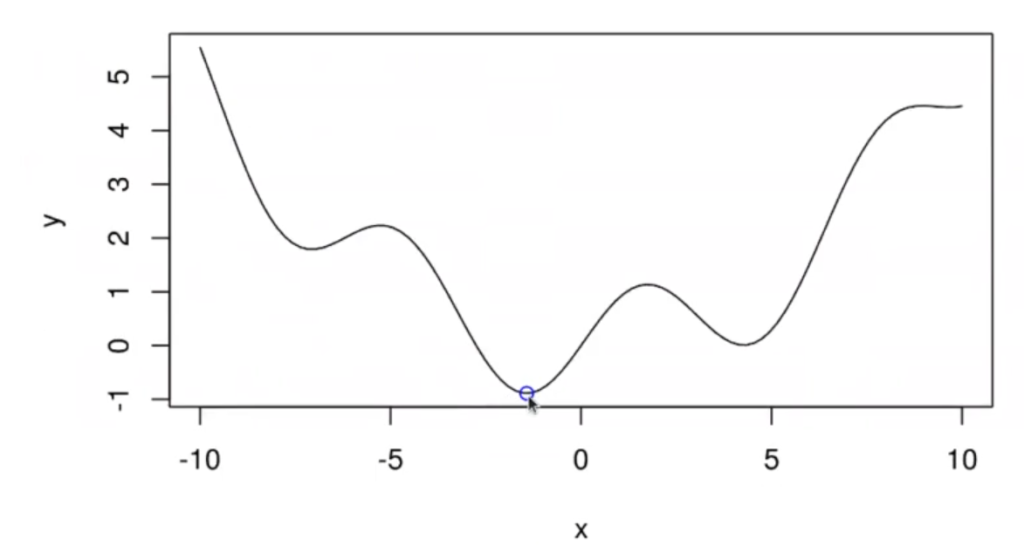
Segunda función
La segunda de las funciones para optimización en R de la que hablaremos es un poco más compleja, ya que es de dos dimensiones:
In 1: #myfunc30 <- function(x1, x2) (sin(x1 + 0.01) *sin(x2)/(x1(x2-0.005))
myfunc3D <- function (x1,x2) {log(abs((sin(x1) (x2 * x1 + 3)) ^ 2 * cos(x2)))}
plotMyFunc <- function (mytunc, margin) {
x <- seq(margin[1]. margin[2]. length = 100)
y <- seq(margin[1], margin[2]. length = 100)
z <- outer (x, y, myfunc)
image (x, y, z, col = terrain.colors (39))
contour (x, y, z, add = T)
}
myfuncVector <- function(x) { myfunc3D (x[1], x[2])}
In [ ]: o <- optim (c(5,1), myfuncVector, hessian = TRUE)
oEl resultado sería el siguiente:
$par
6,28318530717959
1,5707963267949
$value
-104.113243291428
$counts
function: 329 gradient: <NA>
$convergence
0
$message
NULL
$hessian
Vemos que en el primer ejemplo utilizamos la función optimize, y en este segundo caso, utilizamos optim. Ambas cumplen el mismo objetivo, solo que en el primer caso se utiliza para funciones de una dimensión, mientras que en el segundo se utiliza optim para resolver funciones de dos dimensiones.
La gráfica de esta función quedaría así:
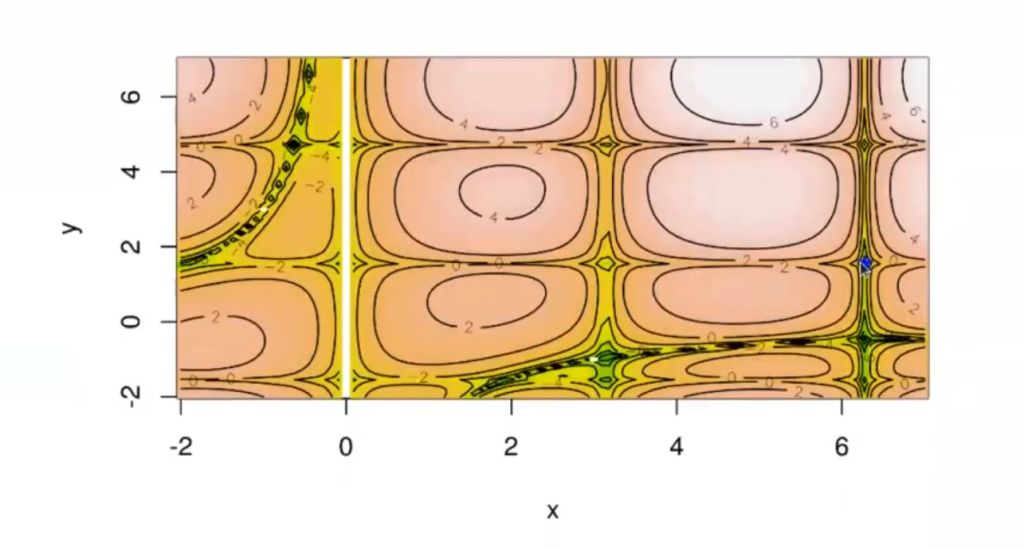
Sabemos que las funciones para optimización en R son un tema mucho más amplio que puede llegar a ser abrumador. Si te gustaría continuar formándote con la guía de un profesional en la materia, no te pierdas nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En poco tiempo, dominarás la teoría y la práctica de ese mundillo para incursionar rápidamente en el mercado laboral con mejores oportunidades de empleo. ¡Anímate a solicitar más información para descubrir cómo puedes cambiar tu vida!







