Los sistemas de ecuaciones son conjuntos de ecuaciones en cuyo interior se alojan las mismas variables. Las soluciones a estos sistemas de ecuaciones generalmente consisten en asignar valores a las variables, de modo que estas satisfagan cada ecuación. Su solución viene dada por el hallazgo de todas las soluciones dentro del sistema.
¿Qué son los sistemas de ecuaciones?
Un sistema de m ecuaciones (como vemos en la imagen, donde tenemos una fila, otra fila y otras m filas) con n incógnitas (que en la imagen se ven representadas por las columnas) se puede escribir de la siguiente manera:
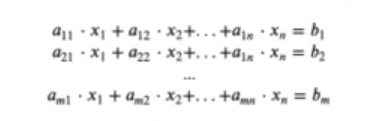
Como hemos visto anteriormente, también podemos escribirlo de la siguiente forma, que es la forma matricial:
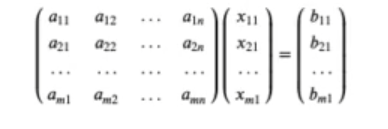
Tenemos, por tanto, la primera ecuación en la primera fila, la segunda ecuación en la segunda fila, la tercera ecuación en la tercera fila, y así sucesivamente hasta las n filas.
Toda esta matriz se resume como A . X = B
También tenemos el vector columna, que tiene los componentes del vector x. Después, tenemos el vector resultante B.
Se llama matriz de coeficientes a:

Y matriz ampliada a:

Reescribiendo el sistema de ecuaciones
Aquí vamos a aplicar lo que ya sabemos para reescribirlo usando una forma más compacta. Para ello, tenemos en cuenta la matriz de coeficientes:
Ax = B
Donde A es una matriz de mxn, x y B son dos vectores columna de longitud n. Para poder resolver esta ecuación Ax = B, debemos despejar x:
Ax = B
A-1 Ax = A-1 B
Ix = A-1 B
x = A-1 B
Determinar si los sistemas de ecuaciones se pueden resolver
Los sistemas de ecuaciones lineales pueden tener:
- Una única solución → sistema compatible determinado
- Infinitas soluciones → sistema compatible indeterminado
- Sin solución → sistema incompatible
Sistema compatible determinado
Los sistemas de ecuaciones lineales serán sistemas compatibles determinados, es decir, tendrán una única solución cuando el determinante de la matriz A sea igual a 0.
det (A) ≠ 0 → Sistema compatible determinado
¿Quieres seguir aprendiendo?
Ahora que sabes algunas cosillas sobre los sistemas de ecuaciones, puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Podrás acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!











