El gráfico Q-Q en estadística Big Data es una de las herramientas de esquematización para los macrodatos que se han estudiado por medio de estadísticos que pretendan, a través de una muestra, calcular el comportamiento de una población.
Además, el análisis exploratorio de datos es el primer paso que todo data scientist debe realizar, ya que de esta manera podrá ver qué se le puede preguntar a los datos y qué información se podrá sacar de ellos una vez los resultados hayan sido arrojados.
Por esta razón, conocer la diversidad de alternativas para el desarrollo de un estudio estadístico también se plantea como una base necesaria en un data scientist y, por ello, en este post, te exponemos todo lo relacionado con el gráfico Q-Q en estadística Big Data.
Gráfico Q-Q en estadística Big Data
El grafico Q-Q en estadística Big Data se utiliza para comparar dos distribuciones al ilustrar sus percentiles una contra la otra. Por ello, generalmente se utiliza para comparar si una variable sigue una distribución gausiana, es decir, la distribución normal que es, posiblemente, la distribución de probabilidad más utilizada, ya que su importancia radica en el teorema central del límite.
De manera que el gráfico Q-Q en estadística Big Data se presenta con gran frecuencia en este campo de los estadístico para el manejo de los macrodatos. A continuación, te presentamos cómo se desenvuelve este tipo de gráfico según las operaciones que esquematice:
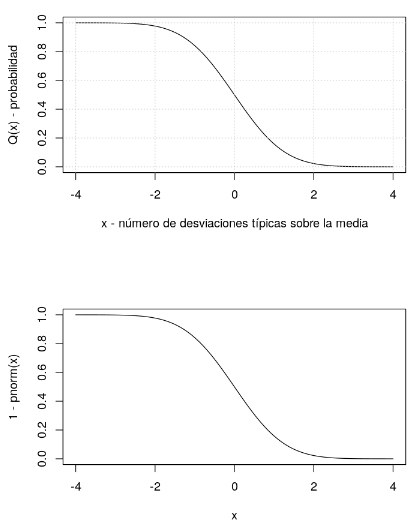
x<-seq(-4,4,length.out=1000) plot(x,pnorm(x,lower.tail = F),t="l",ylab="Q(x) - probabilidad",xlab="x - número de desviaciones típicas sobre la media") grid() # Es equivalente a: plot(x,1-pnorm(x),t="l")
Esta operación se ilustraría de la siguiente forma:
numSamples<-10
#Empezamos con una variable aleatoria ordenada
var_random <-sort(runif(numSamples,min=-5,max=5))
#calculamos su probabilidad de que P(X>x)
p = ((numSamples-1):0)/numSamples
#Basandonos en esta probabilidad, calculamos cual sería su valor si fuera gaussiana
z<-qnorm(p,lower.tail = F)
matrix(c(var_random,p,z),nrow=3,byrow = T,
dimnames=list(c("x","P(X>x) o Q(x)","valor esperado de x si fuera gaussiana"),NULL))
A matrix: 3 × 10 of type dbl:

#plot(p,var_random)
#El gráfico QQ sería:
plot(z,var_random,
xlab="número de desviaciones típicas sobre la media teórica",
ylab="valores reales")
Estas desviaciones típicas se esquematizarían de la siguiente manera:
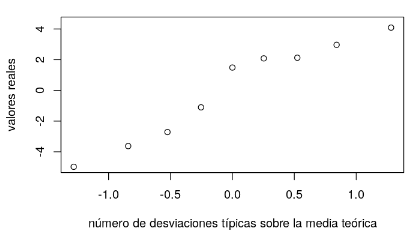
Por otra parte, en cuanto a la distribución gaussiana que suele trabajarse, en este caso, evidentemente, el gráfico Q-Q de una variable gaussiana es una línea recta. A continuación, te exponemos la operación y su respectiva esquematización Q-Q:
numSamples<-1000
gauss_random <-sort(rnorm(numSamples,mean=5,sd=3))
p = ((numSamples-1):0)/numSamples
z<-qnorm(p,lower.tail = F)
plot(z,gauss_random,
xlab="número de desviaciones típicas sobre la media teoórica",
ylab="valores reales")
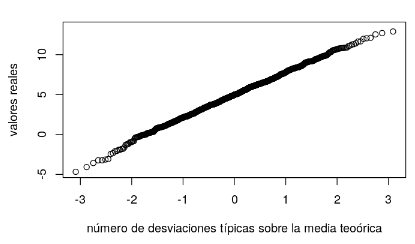
Ahora bien, existe una función para hacer esto mismo:
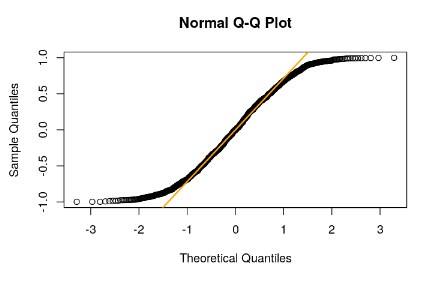
qqnorm(gauss_random) qqline(gauss_random, col = 'orange', lwd =2)
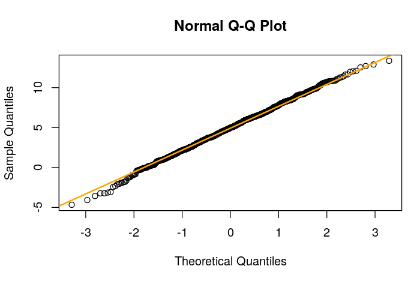
unif1<-subset(myRandomDataFrame,numFunctions==1)$val qqnorm(unif1) qqline(unif1, col = 'orange', lwd =2)
¿Cómo instruirse en Big Data?
Por medio de este post te has podido familiarizar con todo lo relacionado con el gráfico Q-Q en estadística Big Data a partir de diferentes operaciones que lo utilizan para esquematizar los resultados arrojados. Desde KeepCoding esperamos que esta información haya sido de ayuda para tu procesamiento de datos y te animamos a continuar en este mundo del manejo Big Data.
Por ello, si lo que quieres es aprender más sobre el Big Data y sus herramientas, te recomendamos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. A través de este bootcamp, aprenderás a dominar los conocimientos necesarios para implantar cualquier tipo de arquitectura y para los desarrollos necesarios, tanto técnicos como analíticos, dentro del mundo del Big Data. ¡No lo dudes más e inscríbete ya para convertirte en un experto del sector IT!











