Representar las variables en un ejercicio de boosted trees

En este post vamos a representar la importancia de las variables en un ejercicio de boosted trees. Recordemos que la importancia de las variables es un aspecto que solo se puede medir en los algoritmos basados en árboles. En este caso, tenemos un ejercicio de boosted trees o gradient boosting para ejemplificar el modo en el que funciona esta característica.

Los boosted trees son un proceso iterativo basado en la combinación lineal de algoritmos simples, ya sean de weak regression o classifiers, entre los que están los árboles de decisión.

Los boosted trees funcionan con un número de árboles mayor que los árboles individuales.

Si bien el gradient boosting es aplicable a cualquier algoritmo de machine learning, se suele usar con árboles. Sumado a esto, en scikit learn se puede hacer una implementación directamente de los boosted trees, pero en este caso la importancia sí funciona exclusivamente con algoritmos basados en árboles, como los random forest, no con otro tipo de algoritmos.

Importancia de las variables en un ejercicio de boosted trees

La importancia de las variables está implementada directamente en scikit learn porque el gradient boosting funciona con árboles. No le podemos pasar otro algoritmo que no sean árboles.

Veamos:

#importancia de las variables en un ejercicio de boosted trees
importances = bt.feature_importances_
importances = importances np.max (importances)

indices = np.argsort (importances) [ : : - 1]

plt.figure (figsize = (10, 10))
plt.barh (range (X_train.shape [1]), importances [indices]]
plt.yticks (range (X_train.shape [1]), features [indices])
plt.show ()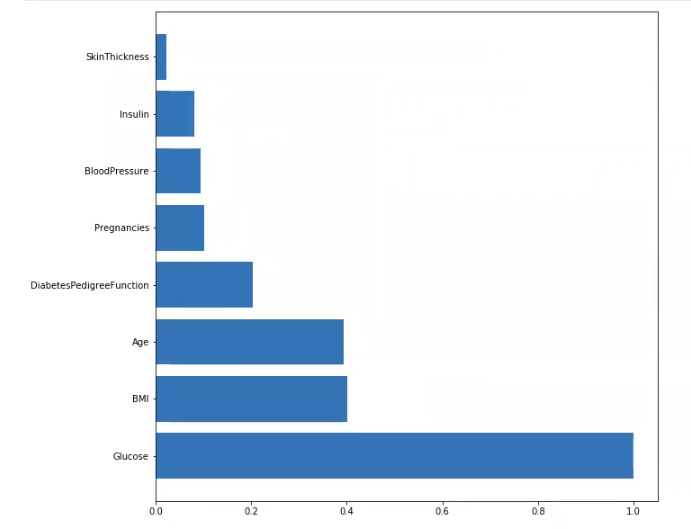

El resultado de este ejercicio sobre la importancia de las variables en un ejemplo de boosted trees nos muestra que la variable más importante es la glucosa.

Lo que podemos hacer también con este tipo de modelo es representar la dependencia de cada característica con la variable objetivo o variable target, que es algo que no podemos hacer en otros modelos:

#importancia de las variables en un ejercicio de boosted trees
from sklearn. inspection import plot partial_dependence

importances = bt.feature importances_
importances = importances / np.max (importances)
indices = np.argsort (importances) [ : : - 1]

plot partial dependence (bt, X_train, indices, feature_names = features, percentiles = (0.0, 1.0), n_cols = 4)
fig = plt.gcf ()
fig.set_size_inches (10, 15)
plt.show ()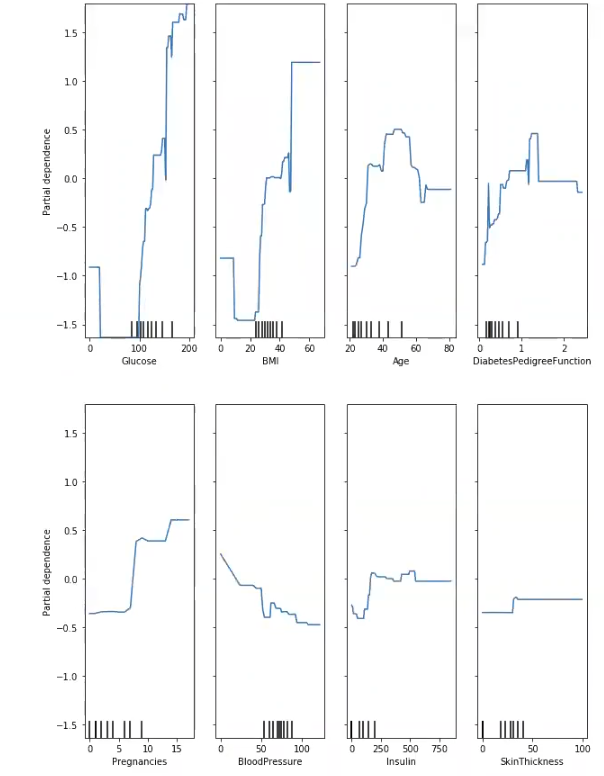

Vemos cómo, en nuestro ejemplo de representar la importancia de las variables en un ejercicio de boosted trees, evoluciona la dependencia parcial a medida que aumentan cada una de las características predichas.

RandomizedSearchCV

Ahora, para seguir con nuestra tarea de representar la importancia de las variables en un ejercicio de boosted trees, lanzamos el RandomizedSearchCV.

El RandomizedSearchCV es una función que implementa un método de ajuste y puntuación. Esta nos ayuda a encontrar los conjuntos de hiperparámetros que dan mejor resultado, pasando aleatoriamente el conjunto de hiperparámetros y calculando la puntuación, lo cual proporciona el mejor conjunto de hiperparámetros que nos brinda la mejor puntuación como salida.

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model selection import RandomizedSearchCV

Niterations = [25, 50, 75, 100,125, 150, 175, 200, 300]
learningRate = [0.5, 0.1, 0.05, 0.01]
#mantenemos max depth estático: max depth-2

param grid = {'n estimators': Niterations, 'learning_rate': learningRate }
grid = RandomizedSearchCV (GradientoostingClassifier (random_state = 0, max_depth = 2), param_distributions = param_grid, cv = 5, verbose = 1)
grid.fit (X_train, y_train)
print("best mean cross-validation score: {: .3f}".format (grid.best_score_))
print ("best parameters: {}".format (grid.best params_))

Este último proceso que hemos hecho con RandomizedSearchCV podríamos haberlo hecho con GridSearchCV. No obstante, existe una diferencia entre los resultados que presenta el GridSearchCV frente al RandomizedSearchCV, ya que este último ha tardado menos en finalizar.

Veamos el resultado de un GridSearchCV:

Este último ha tardado más porque el primero no ha probado todas, solo ha probado algunas.

Entonces, lo que nos está diciendo el RandomizedSearchCV es que, de un subconjunto de datos total, el mejor resultado es el que se presenta.

El RandomizedSearchCV se usa cuando tenemos que hacer barridos muy grandes.

¿Qué sigue?

Tras aprender la importancia de las variables en un ejercicio de boosted trees, puedes seguir aprendiendo por medio mucho más sobre este sector en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva que te preparará de manera óptima para el mundo laboral. ¡Anímate a cambiar tu futuro y solicita más información ahora!