El LDA para clases múltiples es donde podemos sacarle verdadero partido al LDA, ya que para clasificar 2 clases es prácticamente igual a la regresión logística. Cuando tenemos múltiples clases, como en el ejemplo del conjunto de datos Iris, donde teníamos tres clases (versicolor, setosa y virgínica), la idea es la misma: encontrar un plano sobre el que proyectar. Para eso utilizaremos el análisis discriminante lineal o LDA para clases múltiples con sus respectivas funciones discriminantes.
¿Cómo funciona el LDA para clases múltiples?
Consideremos que tenemos dos clases (LDA para clases múltiples) y un vector sobre el que proyectaremos las dos clases, de forma que podamos resumir el valor de cada muestra en una sola dimensión.
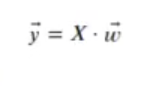
Donde:
- X son los datos que queremos clasificar X E RNxp (X tiene N siglas y p columnas)
- w es el vector de proyección, w E RpxI
- y son los datos proyectados, y E RNxI
Lo que queremos es que los datos proyectados se separen al final entre todas las clases lo máximo posible.
Podemos generalizar a K clases el problema, suponiendo que y tiene más columnas, una por cada clase que queremos clasificar:
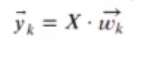
- wk es el vector de proyección, w E RpxI que diferencia la clase k del resto
- yk son los datos proyectados que maximizan la separación entre la clase k y el resto, yk E RNxI
Podemos crear la matriz Y combinando todas las yk:
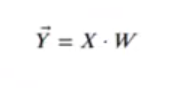
- W es la matriz de proyección, w E RpxK
- Y son los datos proyectados de forma que cada columna k maximiza la separación entre la clase k y el resto, Y E RNxK
Recordemos que Fisher lo que busca es el máximo del cociente:
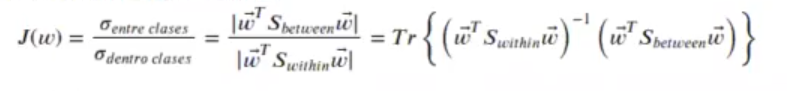
Definimos la media global y para cada clase:
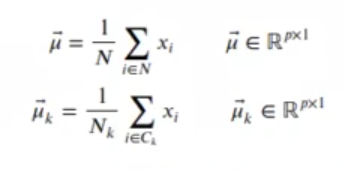
Sbetween es la varianza que hay entre clases, cómo se separa cada clase de la media global.
Para dos clases era:
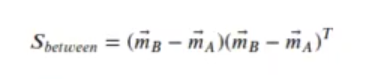
La generalización para K clases (LDA para clases múltiples) es:
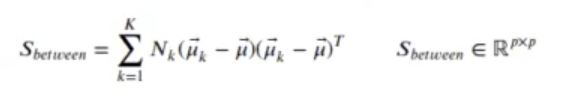
Donde Swithin es la suma de las varianzas de cada grupo. Como varían las muestras dentro de cada clase, para dos clases era:
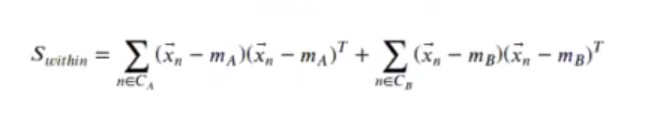
La generalización para K clases es:
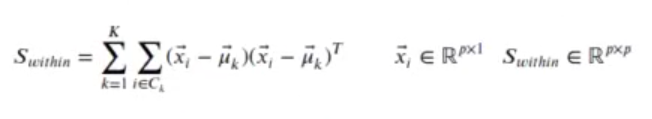
El máximo de J(w) se consigue cuando:
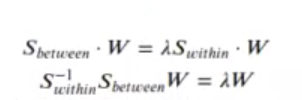
La solución viene dada por los autovectores, cuyos K – 1 autovalores son mayores.
Como hemos visto, el LDA es muchísimo más útil para clases múltiples que para clases individuales o solamente para dos clases. Recuerda que si quieres seguir aprendiendo sobre estas temáticas, aquí tenemos la mejor opción para ti: el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Se trata de una formación intensiva de 8 meses en la que adquirirás todos los conocimientos necesarios para incursionar rápidamente en el mercado laboral. ¡Solicita más información y emprende tu camino hacia el éxito profesional!







