¿Sabes qué relación existe entre los perceptrones y las ecuaciones lineales? En este artículo te lo contamos.
El perceptrón
Los problemas de machine learning se pueden clasificar en función de múltiples aspectos. Nosotros nos hemos centrado principalmente en la categoría de supervised learning y, en concreto, hemos visto las regresiones y los algoritmos de clasificación. En este pequeño aperitivo de redes neuronales vamos a ver cómo se relacionan los perceptrones y las ecuaciones lineales y la importancia de las funciones lineales en el ámbito del machine learning.
Si nos piden que pensemos en un problema de clasificación, hay múltiples problemas que se nos pueden venir a la mente cuando hablamos de problemas de clasificación, por ejemplo:
- Clasificar si un email es SPAM o NO SPAM.
- Clasificar si un libro trata sobre fantasía, aventura, etc.
- Clasificar si un objeto en una imagen es un perro o un gato.
Dado el caso en el que queramos clasificarlo en solo 2 categorías, este se convertiría en un problema BINARIO. De modo que:
- Problema binario: 2 categorías.
- Problema no binario: N categorías (dentro hay más clasificaciones que se suelen hacer).
Todo esto está muy bien y se entiende a la perfección. Sin embargo, no hemos hablado de cómo se relacionan los perceptrones y las ecuaciones lineales. A continuación entramos en este tema.
Los perceptrones y las ecuaciones lineales
Para entender mejor esto de los perceptrones y las ecuaciones lineales, imagínate un problema de clasificación binario, por ejemplo, clasificar si un estudiante va a entrar en la universidad a partir de su nota media durante bachiller (Grades) y de su nota media de selectividad (Test). El objetivo es conseguir dibujar una línea en nuestros datos, llamada boundary line, que nos separe este conjunto de datos:
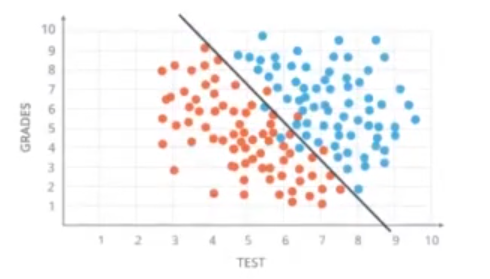
Como ya hemos visto, la ecuación de una función lineal (escrita en forma vectorial) viene definida por:
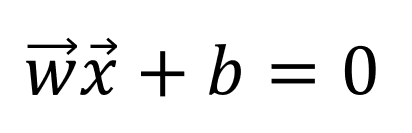
Escrita para 2 variables x1 y x2:
w1 x1 + w2 x2 + b = 0
Esta ecuación la podemos representar gráficamente de una forma muy sencilla, que nos ayudará a entender la unidad básica de las redes neuronales, los perceptrones:
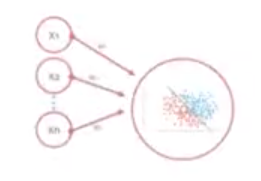
El parámetro b de nuestra ecuación, como ya hemos visto, se denomina bias y debe tenerse en cuenta a la hora de representar dicha ecuación de una forma gráfica; por tanto:
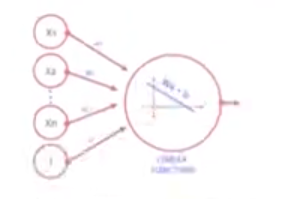
Ya hemos conseguido representar gráficamente nuestra ecuación lineal, pero las redes neuronales necesitan algo que entiendan. En este caso es una probabilidad, por lo que añadiremos un bloque más al final de este perceptrón, que denominaremos función de activación.
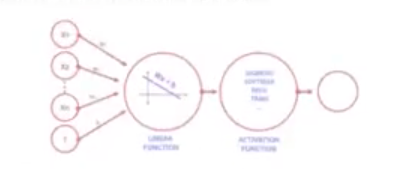
Las funciones de activación son muy importantes para que una red neuronal aprenda. Su principal objetivo es convertir un input en una señal de salida, esta señal de salida como input para el siguiente nodo, etc. Existen diferentes tipos de funciones de activación y debemos usar una u otra dependiendo de nuestro problema.
Si aplicamos una función de salida llamada sigmoid a la salida de nuestra ecuación Wx + b, convertimos el resultado de nuestra ecuación a un valor entre 0 y 1, por ejemplo:
σ (x) = 1 / 1 + e-x
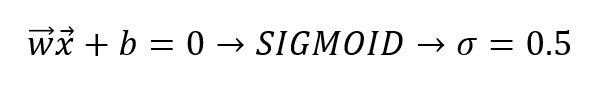
Por tanto, si volvemos a representar de forma gráfica la figura anterior ,obtenemos:
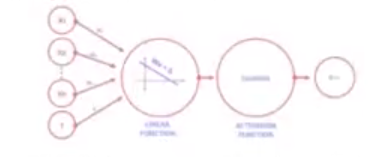
Si convertimos esta representación básica en formato matemático, teniendo en cuenta que y_pred es el valor de nuestra predicción para un input dado, obtenemos:
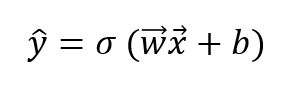
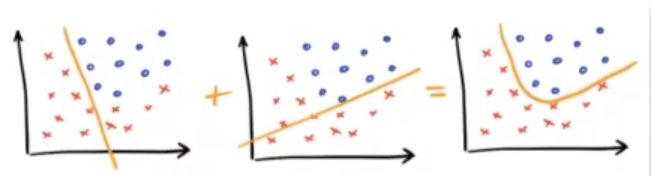
Y esta ecuación es la que rige el compartimiento de los perceptrones, que son la unidad básica para las redes neuronales. Sí, la red neuronal está construida a partir de funciones lineales que, al combinarlas, nos permiten modelar nuestro problema como si fuera no lineal. Así pues, podemos relacionar los perceptrones y las ecuaciones lineales.
¿Quieres seguir aprendiendo?
Ahora que has aprendido todo lo necesario sobre los perceptrones y las ecuaciones lineales, puedes seguir formándote en el mundo del Big Data y convertirte en un experto en el sector. Para acceder a una de las disciplinas más demandadas del mundo laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra e intensiva de alta calidad en la que adquirirás, en unos pocos meses, todos los conocimientos prácitcos y teóricos que te ayudarán a obtener tu trabajo ideal. ¡Entra ya para solicitar información y da el paso que cambiará tu carrera!







