¿Sabías que es posible crear un mapa de correlación entre variables? La correlación entre variables es un proceso que implica la relación entre dos variables relacionadas linealmente. Ambas variables tendrán coeficientes de correlación que permitirán hacer una representación gráfica por medio de un mapa de correlación entre variables.
¿Qué es la correlación de variables?
Las variables dentro de un dataset pueden estar correlacionadas por diversas razones, entre ellas:
- Una variable podría causar o depender de los valores de otra variable.
- Una variable podría estar ligeramente asociada a otra variable.
- Dos variables podrían depender de una tercera variable desconocida.
Existen tres tipos de correlaciones entre variables:
- Correlación positiva: cuando ambas variables se mueven en la misma dirección.
- Correlación neutra: cuando no hay relación en el cambio de las variables.
- Correlación negativa: cuando las variables cambian en direcciones opuestas, por lo que cuando el valor de una variable aumenta, los valores de las otras variables disminuyen.
¿Cómo hacer un mapa de correlación entre variables?
Veamos cómo funciona el mapa de correlación entre variables por medio de un ejercicio práctico:
#mapa de correlación entre variables
import seaborn as sns
#Compute the correlation matrix
corr = np.abs (data.drop (['churn'], axis = 1).corr ())
# Generate a mask for the upper triangle
mask = np. zeros_like (corr, dtype = np.bool) mask [np.triu_indices_ from (mask)] =True
# Set up the matplotlib figure
f, ax = plt.subplots (figsize = (12, 10))
#Draw the heatmap with the mask and correct aspect ratio
sns.heatmap (corr, mask = mask, vmin = 0.0, vmax = 1.0, center = 0.5, linewidths = 1, cmap = "YLGnBu", cbar_kws = ("shrink": 8})
plt.show()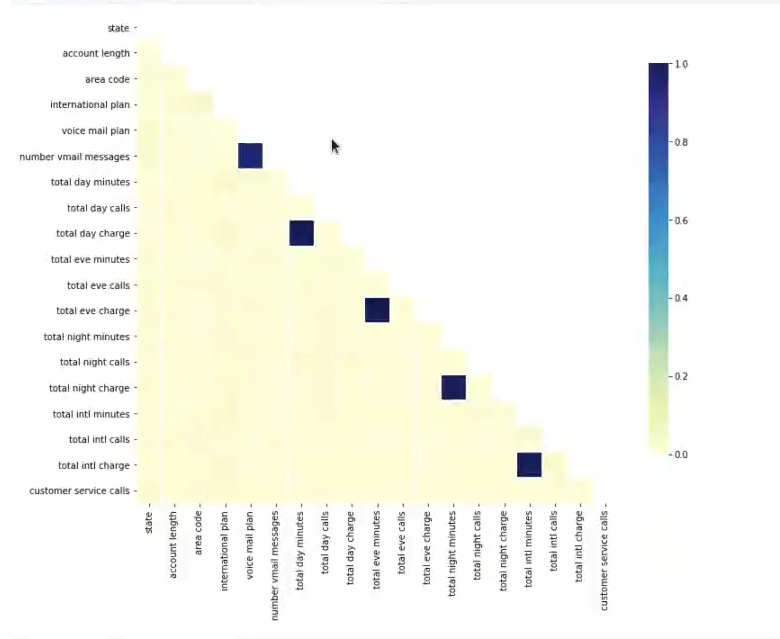
#mapa de correlación entre variables
#Create correlation matrix
corr_matrix = data.corr ().abs ()
#Select upper triangle of correlation matrix
upper = corr_matrix.where (np.triu (np.ones (corr_matrix.shape), k = 1).astype (np.bool))
#Find index of feature columns with correlation greater than 0.95
pairs np.where (upper > 0.95)
fx = data.columns [pairs [0]]
fy= data.columns [pairs [1]]
i = 1
plt.figure (figsize = (22, 4))
for f1, f2 in zip (fx, fy):
plt.subplot(1, 5, i)
plt.scatter (data [f1], data [f2], c = data ['churn'], cmap = cm_bright, alpha = 0.25)
plt.xlabel (f1)
plt.ylabel (f2)
plt.grid ()
plt.tight_layout ()
i+ = 1
plt.show ()
Lo que haremos es generar la matriz de correlación. Luego seleccionamos el triángulo superior; no lo podemos pintar entero porque es una matriz muy grande.
Lo siguiente que haremos es pintar para aquellas variables con un grado de correlación mayor que el umbral, que en este caso es 0.95, hacer un scatter plot y ver qué tipo de relación tenemos.
Aquí vemos cómo, por ejemplo, la matriz total day charges con total day minutes tiene una correlación completamente lineal, prácticamente es perfecta. Y lo mismo sucede con las otras.
En clasificación, las variables correlacionadas no afectan al proceso de clasificación. Sin embargo, dada la correlación extrema (como se ve en la gráfica pintada) y con el objetivo de eliminar variables poco informativas, podemos eliminar algunas columnas. Veamos cómo hacerlo:
#mapa de correlación entre variables
columns_to_drop = ['total day minutes', 'total eve minutes', 'total night minutes', 'total intl minutes']
data.drop (columns_to_drop, axis = 1, inplace = True) data.head()
¿Quieres seguir aprendiendo?
Para que cumplas tus sueños y sigas aprendiendo sobre el mundo tecnológico, que ofrece excelentes oportunidades para desarrolladores y programadores, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación intensiva adquirirás todos los conocimientos teóricos y prácticos para que sigas tu camino hacia el éxito.
Tendrás, además, a los mejores profesionales acompañándote en tu proceso formativo y apoyándote en todo lo que necesites. ¡No esperes más para obtener lo que quieres y solicita más información ahora!











