Con la constante generación de grandes volúmenes de datos de manera simultánea y masiva, ha surgido la necesidad de contar con herramientas como las matrices en estadística Big Data porque gracias a ellas la organización de los datos se facilita enormemente.
En efecto, dominar cada una de estas opciones forma parte de la tarea de un data scientist. Conocer este tipo de estrategias para la resolución de los problemas con los datos mejorará tu trabajo. Por ello, en este post, te presentamos qué son las matrices en estadística Big Data.

¿Qué son las matrices en estadística Big Data?
Las matrices en estadística Big Data se conocen como un tipo de organización de los datos, de manera que sea mucho más comprensible el procesamiento de la información y los resultados arrojados.
Ahora, podrás crear matrices con la función matrix. Así, una matriz es la que se comporta como parámetros de entrada que recibe un vector y el número de columnas (ncol) o filas (nrow). Por otra parte, existe un parámetro opcional (byrow), gracias al que se indica si la matriz se va a rellenar por filas o por columnas (valor por defecto).
1:12
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
In [133]:
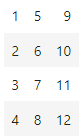
m1<-matrix(c(1:12),ncol=3) m1
A matrix: 4 × 3 of type int
?matrix
In [135]:
m2<-matrix(c(1:12),ncol=3,byrow=T) m2
A matrix: 4 × 3 of type int:

La dimensión del array se puede ver con la función dim() o con str():
dim(m1)
- 4
- 3
length(m1)
12
str(m2)
int [1:4, 1:3] 1 4 7 10 2 5 8 11 3 6 ...
Acceso a las matrices en estadística Big Data
En cuanto al acceso, este se realiza igual que como funciona con los vectores. Sin embargo, en esta oportunidad, podrás contar con dos dimensiones. A continuación, te mostramos un breve ejemplo:
m1[1,3]
9
m1[,2]
- 5
- 6
- 7
- 8
En suma, también podrás dar nombres a las filas y columnas para luego poder acceder utilizando el nombre.
?paste0
paste0("row",1:4)
- ‘row1’
- ‘row2’
- ‘row3’
- ‘row4’
colnames(m1)<-paste0("col",1:3)
rownames(m1)<-paste0("row",1:4)
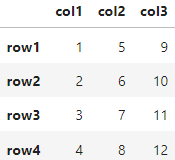
m1
A matrix: 4 × 3 of type int:
paste("El valor de 'row1' y 'col3' es:",m1["row1","col3"])
‘El valor de \’row1\’ y \’col3\’ es: 9′.
m1["row1",]

Las funciones colnames y rownames.
// matriz estadistica colnames(m1)
- ‘col1’
- ‘col2’
- ‘col3’
Operaciones con matrices
Las matrices en estadística Big Data también pueden prestarse para realizar ciertas operaciones, como las que te presentamos a continuación por medio de un ejemplo:
Álgebra lineal básica
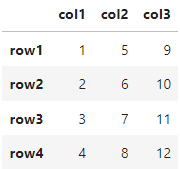
m1
A matrix: 4 × 3 of type int
Transpuesta
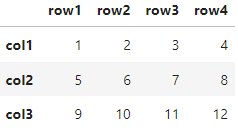
t(m1)
A matrix: 3 × 4 of type int
Suma de constante
m1+10
A matrix: 4 × 3 of type dbl:
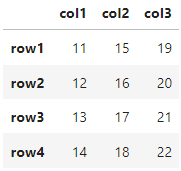
Suma de matrices
m1+m2
A matrix: 4 × 3 of type int
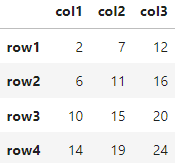
Multiplicación de matrices
m1 %*% matrix(rep(1,12),nrow=3)
A matrix: 4 × 4 of type dbl
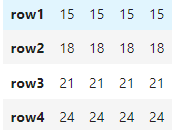
rep("a",5)
- ‘a’
- ‘a’
- ‘a’
- ‘a’
- ‘a’
Submatrices
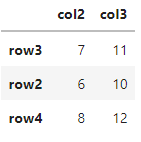
m1[2:4,2:3]
A matrix: 3 × 2 of type int
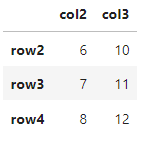
m1[c(3,2,4),2:3]
A matrix: 3 × 2 of type int
Aplicaciones prácticas e integración tecnológica
Las matrices en estadística Big Data son muy importantes en el manejo de datos relacionados con redes sociales, análisis financiero y estudios epidemiológicos, donde la rapidez y precisión son cruciales. Además, su integración con herramientas como Apache Spark y plataformas como Hadoop permiten que los datos se procesen de manera correcta, apoyando operaciones como map-reduce que son fundamentales en el entorno de Big Data.
Desafíos y estrategias de optimización
A pesar de su utilidad, las matrices en estadística Big Data se enfrentan a desafíos en términos de escalabilidad y gestión de memoria, especialmente con datasets extremadamente grandes. Debes tener presente que la optimización de almacenamiento y el uso de técnicas de descomposición de matrices pueden ayudar a mitigar estos problemas, mejorando significativamente el rendimiento de las operaciones de datos.
Comparación con otras estructuras de datos
Si las comparamos con otras estructuras de datos, las matrices ofrecen una manera más estructurada y matemáticamente completa para manejar datos numéricos. Sin embargo, estructuras como los DataFrames o documentos JSON pueden ser más adecuados para datos heterogéneos o no estructurados.
En este post te hemos explicado qué son las matrices en estadística Big Data, algunas de sus funciones y cómo realizar operaciones con ellas. No obstante, este tipo de conocimiento exige de una práctica constante para desarrollarse adecuadamente. Por ello, te aconsejamos practicar por medio del método de ensayo y error hasta que te conviertas en un experto.
Para ello, desde KeepCoding te ofrecemos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. En él aprenderás todo lo necesario sobre el entorno de programación y sobre fuentes de datos múltiples, visualización de relaciones entre valores numéricos (diagramas de dispersión, regresión y clustering), de tipos de datos específicos, como geográficos o mapas de calor, etc.







