En este artículo veremos cómo funciona una matriz inversa usando Gauss, un método empleado para un sistema de ecuaciones lineales que nos permita obtener la matriz deseada.

Matriz inversa usando Gauss

Al igual que el inverso de 5 es 1/5 = 5^-1, dada la matriz A, no puedo calcular 1/A, pero sí A-¹.

La manera usual de calcular la matriz inversa, sobre todo si no es demasiado grande, es mediante determinantes, aunque hay otro modo general de calcular la matriz inversa: el método de Gauss.

Dada una matriz A, consideramos la matriz (A | I).
Mediante una serie de transformaciones, tenemos que conseguir transformarla en (I | B).
B = A-¹

Vamos a calcular la inversa de la siguiente matriz usando el método de Gauss, por medio del np.array:

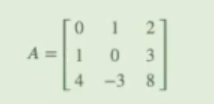
AX = B → X = A-¹ * B

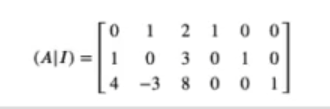
Lo primero que vamos a hacer es añadir a la derecha de la matriz A una matriz identidad y obtendremos (A | I):

AI = np.array ([[0, 1, 2, 1, 0, 0],
                          [1, 0, 3, 0, 1, 0],
                          [4, -3, 8, 0, 0, 1]])

AI

Buscamos hacer transformaciones de modo que obtengamos una matriz con la forma (I | B), donde B será la inversa de A. Lo primero que hacemos es intercambiar la segunda fila con la primera fila:

#Matriz inversa usando Gauss
AI = np.array ([AI[1], AI[0], AI[2]])
AI

#Matriz inversa usando Gauss
fila_1 = np.array ([1,  0,  3,  0,  1,  0])
fila_3 = np.array ([4,  -3,  8,  0,  0,  1])

fila_nueva_3 = -4 * fila_1 + fila_3
print (-4 * fila_1 + fila_3)

AI_ = np.array ([AI[0],
                            AI[1],
                            (-4 * AI[0] + AI[2])])

AI_

[0 -3 -4 0 -4 1]

Queremos hacer 0 el primer elemento de la tercera fila. Para ello, la tercera fila se convertirá en el resultado de multiplicar -4 por la primera fila y sumarle la tercera fila → tercera fila = -4 * (primera fila) + (tercera fila)

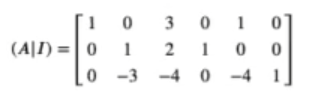
AI_ = np.array ([AI_[0],
                            AI_[1],
                            (3 * AI_[1] + AI_[2])])

AI_

El siguiente paso es hacer 0 el tercer elemento de la primera fila, para ello haremos → primera fila = (primera fila) – 3 * 2 * (tercera fila)

#Matriz inversa usando Gauss
AI: = np.array ([(AI_[0] * 3/2 * AI_[2]),
                            AI_[1],
                            AI_[2]])

AI_

Ahora tenemos que hacer 0 el tercer elemento de la segunda fila → segunda fila = (segunda fila) – (tercera fila)

AI_ = np.array ([AI_[0],
                         (AI_[1] - AI_[2]),
                          AI_[2]])

AI_

Debemos hacer 1 el tercer elemento de la última fila → (tercera fila) = (1/2) * (tercera fila)

AI_ = np.array ([AI_[0],
                           AI_[1],
                           (AI_[2] * 1/2)])

AI_

Por tanto, después de todo, la matriz inversa usando Gauss queda así:

Es decir A-¹:

Si quieres seguir aprendiendo sobre estas interesantes temáticas, puedes seguir nuestro Bootcamp Data Science, donde adquirirás todos los conocimientos necesarios para convertirte en un gran data scientist profesional en poco tiempo. ¡Aprovecha esta oportunidad de triunfar en el mundo IT y solicita más información ahora!