Método de Newton

El método de Newton es un método utilizado para encontrar, de forma iterativa, la raíz de una función.

¿Cómo se desarrolla el método de Newton?

Tenemos la siguiente función:

In [ ]: f_x<- function(x) {x^3}

x<-seq(-9,3,length.out = 180)
y<-f_x(x)

options (repr.plot.height-4, repr.plot.width=6) 
plot(x,y,t="l")
abline (h=0)
grid()
options(repr.plot.height=5, repr.plot.width=8)

plotDerivada<- function(x,color="red")
     delta <- 3
     lines(c(x-delta, x-delta),
               c(f x(x)-delta*3*x^2,f_x(x)+delta*3x^2),
               col-color)
}

plotDerivada(-7)
abline(v=-4.65, col-gray")
plotDerivada(-4.65, color="blue")
abline(v=-3.1,col="gray")
plotDerivada (-3.1, color orange")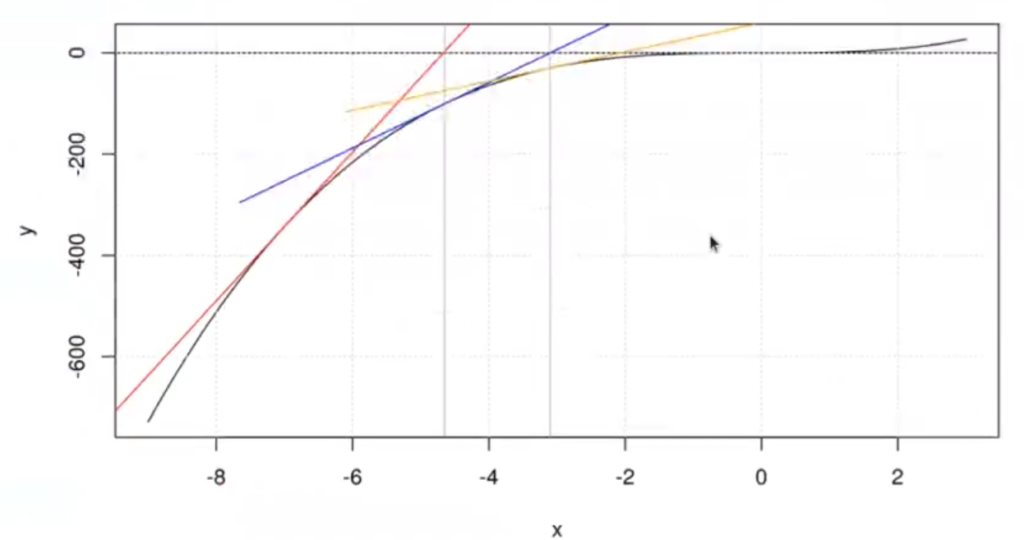

Tenemos que encontrar el cruce por 0 de esta función. Para ello, empezamos en un punto aleatorio, que en nuestro caso es -7 (plotDerivada(-7)). Con ello se pinta la recta de color rojo. Donde cruza esta recta pintamos otra vertical y, en ese mismo punto, se lanza otra derivada. Sale otra recta y hacemos lo mismo que con la anterior, y así infinitas veces hasta que converge a 0.

Este método iterativo aproxima el valor de la función a 0 siguiendo los siguientes pasos:

1. Selecciona un punto inicial: x₀.
2. Traza una línea tangente a la curva, es decir, con pendiente igual a la derivada.
3. Proyectar la línea anterior hasta que corte en y = 0. El valor de x donde corta será el nuevo x₀.
4. Repetir desde el paso 2 hasta que f(x) sea muy cercano a 0.

Estos pasos se pueden simplificar de la siguiente forma: podemos aproximar la función f(x) en un punto x cercano a x₀ de la siguiente forma. Esto se considera una aproximación al desarrollo en serie de Taylor solo con la primera derivada:

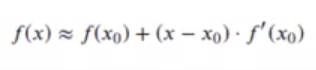
Si igualamos f(x) = 0 y despejamos x:

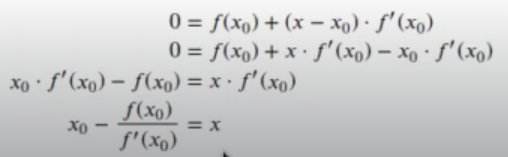
Encontrar el mínimo de una función equivale a encontrar la raíz de su derivada. Es decir, el mínimo siempre se encuentra en f'(x) = 0. Por lo tanto, podemos usar el método de Newton para encontrar el mínimo de una función. Solo hay que reemplazar f(x) por f'(x):

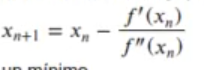
Aplicamos de forma iterativa esa ecuación hasta que alcanzamos un mínimo.

¿Qué te pareció este tema?

Sabemos que temáticas como el método de Newton son algo complicadas de entender, sobre todo porque el mundo del Big Data es demasiado grande y hay miles de cosas por conocer.

Recuerda que desde Keepcoding tenemos a los mejores profesionales en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, listos para acompañarte en tu proceso de formación. En pocos meses podrás instruirte en todos los temas necesarios para incursionar en el mundo laboral. ¡Únete a nosotros y emprendamos juntos este camino lleno de retos y éxito!