Métodos de clustering

¿Sabías que existen diferentes métodos de clustering que puedes usar para ejecutar tus agrupamientos de manera más fácil y óptima?

El clustering es el método por el cual se agrupan entidades en función de sus similitudes. ¿Y qué tipo de similitudes? Eso es precisamente lo que responderemos en este artículo, ya que vamos a evaluar algunos de los métodos de clustering más famosos que existen para poder identificar la forma de agrupar distintos elementos en sus respectivas categorías.

Métodos de clustering: clustering particionado

Métodos de clustering: k-means

Este es el primero y uno de los más famosos métodos de clustering y se basa en centroides. El centroide o centro geométrico es el punto resultante de la media aritmética de la posición de todos los puntos.

1. Elige k centroides al azar.
2. Asigna el elemento al centroide más cercano.
3. Se hace el recálculo de centroides.
4. Se repite desde 2 mientras los centroides se sigan actualizando.

options (repr.plot.height = 4, repr.plot.width = 6, repr.plot.res = 300)

N <- 380
x1 <- c (rnorm (N, mean = 2, sd = 2), rnorm (N, mean = -2, sd = 2), rnorm (N, mean = -5, sd = 1))
x2 <- c (0.4 * x1 + c (rnorm (N, mean = 3, sd = 2), rnorm (N, mean = -3, sd = 1), rnorm (N, mean = 7, sd = 1)))
df <- data.frame (x1, x2)

library (ggplot2)
ggplot (data = df, aes (x = x1, y = x2)) + geom_point (alpha = 0.7)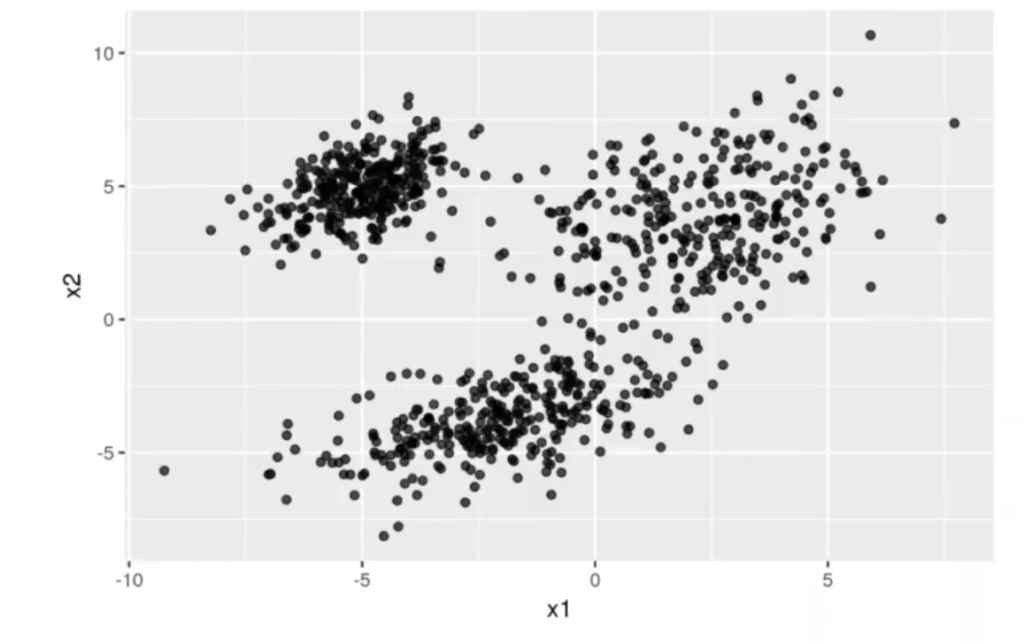

Tenemos una nube de puntos y la idea es que el algoritmo de clustering k-means nos los agrupe. A ojo, podríamos decir que hay tres grupos de puntos.

¿Qué es lo que necesita el primero de los métodos de clustering, el k-means? Este necesita que le digamos cuántos grupos hay, ya que él no se va a inventar esta información.

Lo primero que haremos será definir la función de la distancia euclídea:

mydistance <- function (v1, v2) {
sqrt ((vi [1] - v2 [1]) ^ 2 + [v1 [2] - v2 [2]) ^ 2)
}

assign_points_to_centroid <- function (mydata, centroids) {
groups <- rep (NA, nrow (mydata))
for (i in 1:nrow (mydata)) {
distance_to_centroids[j] <- mydistance (mydata[ i ,] , centroids [ j ,])
}
group[1] <- which.min (distance_to_centroids)
}
group
}

get_new_centroids <- function (mydata, group) { 
k <- length (unique (group))
centroids <- data.frame (x1 = rep (NA, k), x2 = rep (NA, k))
for (i in l : k) {
idx <- which (i == group)
centroids [ i ,] <- colMeans (mydata [idx ,])
}
centroids
}
plot_all <- function (mydata, centroids, group) {
mydata$group <- factor (group)
mydata$centroidx1 <- centroid$x1 [group]
mydata$centroidx2 <- centroids$x2 [group]
ggplot (data = mydata, aes (x = x1, y = x2) + geom_point (color = group, size = 0.5) + geom_point (aes (x = centroidx1, y = centroidx2), shape = " * ", size = 5, color = "purple")
}

centroids <- data.frame (x1 = c (1, 2), x2 = c (1, 1))
#centroids <- data.frame (x1 = c (1, 2, 3), x2 = c (1,1,1))
centroids
group <- assign_points_to_centroid (df, centroids)
plot_all (df, centroids, group)

centroids <- get_new_centroids (df, group)
centroids

x1	x2
<dbl>	<dbl>
1	1
2	1

x1	x2
<dbl>	<dbl>
-3.014215	1.012854
3.321522	3.810731

El centroide es la media de todos los puntos. Nosotros hemos empezado con dos centroides al azar, que se pueden ver identificados por las estrellas moradas en el gráfico. Entre los métodos de clustering que existen, el k-means lo que ha hecho es clasificar en dos los puntos (puntos negros y puntos rojos) a partir de los dos centroides que hemos definido.

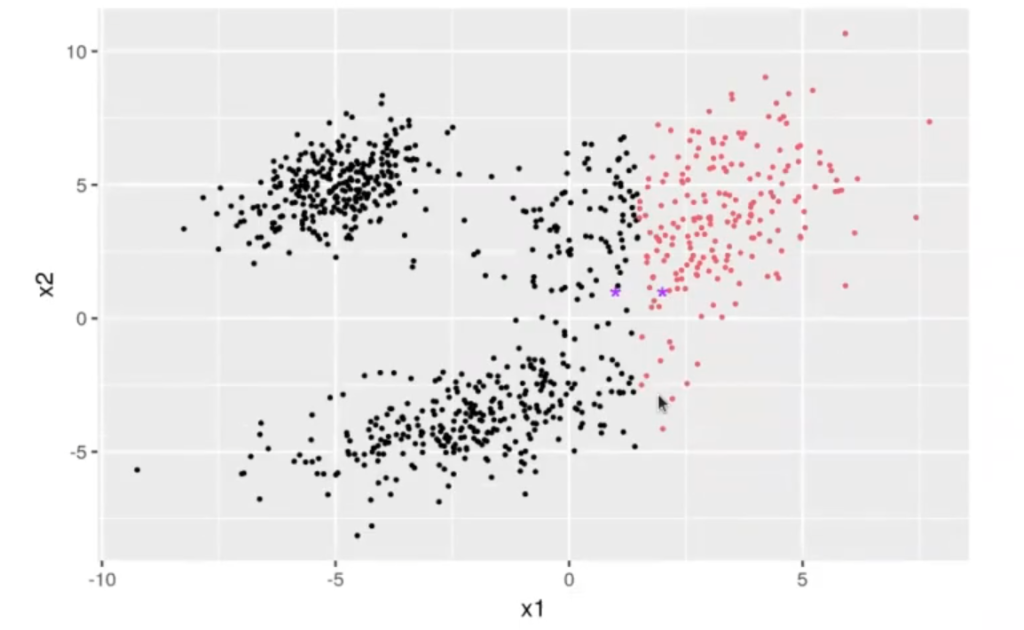
Lo que haremos ahora será calcular el centroide de todos los puntos negros. Estos centroides se calculan con get_new_centroids.

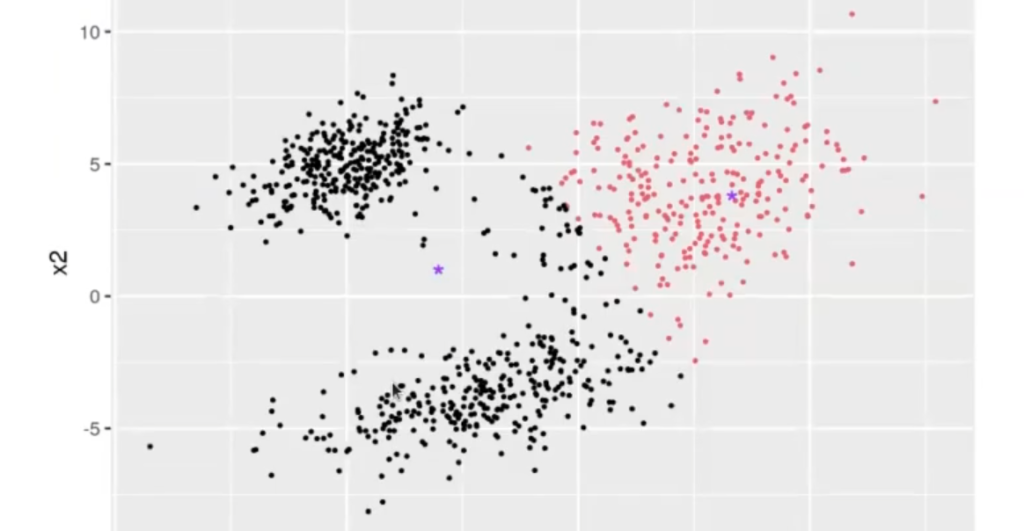
Ahora, nos ha calculado los centroides de los dos puntos de centroides que hemos definido previamente. La tabla cálculo 1 de centroides nos muestra cómo eran antes (primera gráfica) y la tabla cálculo 2 de centroides nos muestra cómo son ahora (gráfico 2).

Este proceso es iterativo.

Este algoritmo lo implementa R:

kmeans (data. frame, k)

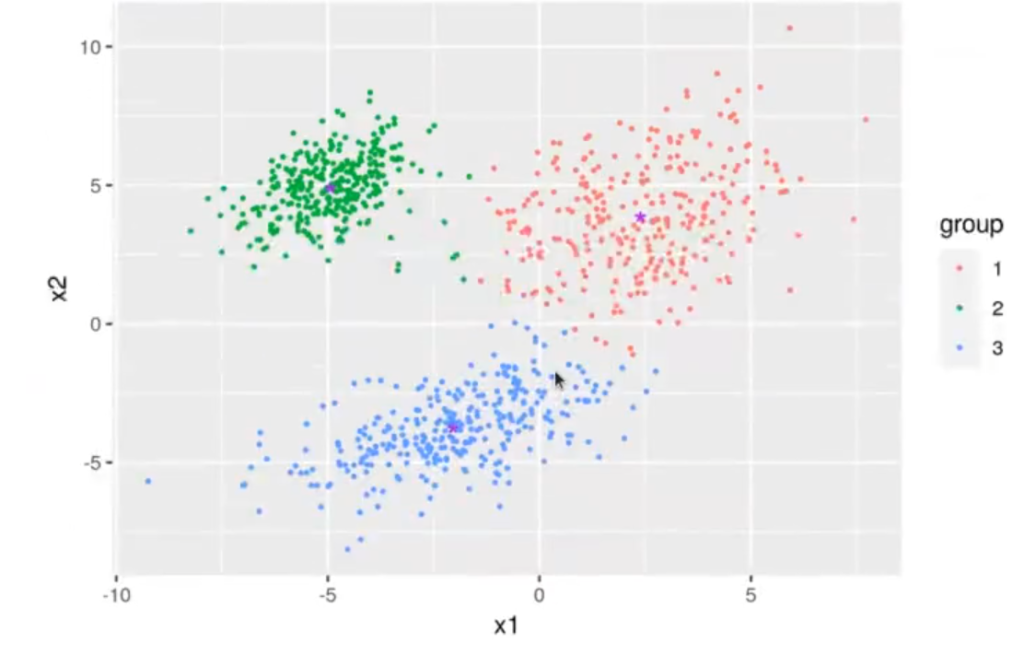
myclust <- kmeans (df, 3)

print ("Los centroides son")

myclust$centers
#myclust$cluster

[1] «Los centroides son»

	x1	x2
1	2.386538	3.871801
2	-4.928351	4.911918
3	-2.038935	-3.760849

mycluster$centers [, "x1"]

1: 2.38653815316614

2: -4.92835087692713

3: -2.03893540198899

str (myclust)

table (myclust$cluster) #contar cuántos clústeres hay en el grupo 1, cuántos en el grupo 2, etc.
myclust$cluster

1	2	3
287	307	306

cl <- factor (myclust$cluster)

clustered <- cbind (df, group = cl)
clustered$centroidx1 <- myclust$centers [group, "x1"]
clustered$centroidx2 <- myclust$centers [group, "x2"]
ggplot (data = clustered, aes (x = x1, y = x2)) + geom_point (aes (color = group), size = 0.5) +
geom_point (aes (x = centroidx1, y = centroidx2), shape = " * ", size = 5, color = "purple")

summary (clustered)

Siempre debemos asignar el clúster a un factor.

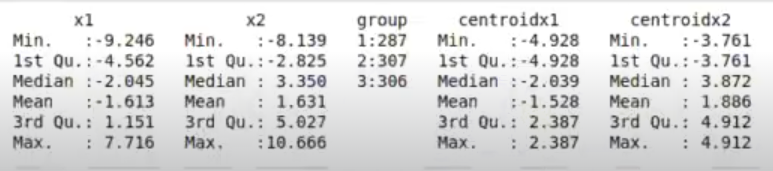
Por último, hemos pintado de un color distinto cada clúster.

¿Qué sigue?

Si quieres seguir aprendiendo sobre métodos de clustering y otros temas relacionados, puedes inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva con la que, en unos pocos meses, dominarás todos los conocimientos teóricos y prácticos necesarios para incursionar en el gran mercado laboral IT. ¡Solicita más información y cambia tu vida!