Existen diversos métodos de filtrado para regresión. En este artículo te contaremos cuáles son algunos de ellos y en qué consisten.

¿Qué encontrarás en este post?

Métodos de filtrado para regresión

Lo primero que haremos para iniciar nuestro ejercicio y mostrar los métodos de filtrado para regresión es cargar las librerías y funciones necesarias:

#Métodos de filtrado para regresión
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
%matplotlib inline

cm = plt.cm.RdBu
cm_bright = ListedColormap (['#FF0000', #0000FF'])

import warnings
warnings.filterwarnings ('ignore')

Mediante un ejemplo sencillo, vamos a analizar los métodos de filtrado para regresión:

Ambos métodos de filtrado para regresión funcionan de manera similar, de variable a variable, es decir, variable A con objetivo, variable B con objetivo, etc. No obstante, f_regression solo coge dependencias lineales, mientras que mutual_info coge todas, pero necesita más datos para funcionar bien.

Ejemplo

Teniendo lo anterior en cuenta, veamos un ejemplo: se tienen tres variables x₁, x₂, x₃, que representan variables aleatorias que se distribuyen uniformemente en el intervalo [0, 1]. La salida depende de estas variables de la forma:

y = x₁ + sin (6 π x₂) + 0.1 N (0, 1)

Esto es:

y depende linealmente de x₁
y depende no linealmente de x₂
y no depende en absoluto de x₃

Por tanto, x₃ es una variable irrelevante para y. Veamos qué nos dicen nuestros test de filtrado para regresión de selección de características:

#Métodos de filtrado para regresión
#Este ejemplo, tomado de:
#http://scikit learn.org/stable/auto_examples/feature selection/plot frost vs whtalaspox-plr-auto examples-feature-selection plot-fest

#importamos los métodos
from sklearn.feature_selection import f_regression, mutual_info_regression

#fabricamos la función y = x1 + sin (6 π x2) + 0.1 N (0, 1)
np.random.seed (0)
X = np.random.rand (1000, 3)
#así representamos la función de arriba
y = x [ : , 0] + np.sin (6 * np.pi X [ : , 1]) + 0.1 * np.random.randn (1000)

f_test, _ = f_regression (X, y)
f_test /= np.max (f_test)

mi = mutual_info_regression (X, y)
mi /= np.max (mi)

plt.figure (figsize = (15, 5))
for i in range (3):
plt.subplot (1, 3, i + 1)

plt.scatter (X [ : , i], y, edgecolor = 'black', s = 20)
plt.xlabel ('$x_ {} $'.format (i + 1), fontsize = 14)
if i == 0:
plt.ylabel ("$y$", fontsize = 14)
plt.title ('F - test = { : . 2f}, MI = { : . 2f}'.format (f_test [ i ], mi[ i ]), fontsize = 16)

plt.show()

Lo primero que haremos es importar los métodos. Posteriormente, vamos a fabricar la función y = x₁ + sin (6 π x₂) + 0.1 N (0, 1) por medio del y = x [ : , 0] + np.sin (6 * np.pi X [ : , 1]) + 0.1 * np.random.randn (1000). Acto seguido, aplicamos f_test sobre x y luego aplicamos mutual_info_regression sobre x, es decir, aplicamos ambos métodos de filtrado para regresión sobre x.

f_regression devuelve dos cosas. Cuando no nos interesa recoger las dos cosas que devuelve, la solución es muy simple: es estándar en Python poner un guion bajo para indicar que el método está devolviendo dos cosas y que tenemos que recoger la segunda, pero la segunda no la vamos a usar, así que la dejamos marcada con un guion bajo para que se sepa que esa es la que no se va a usar, que no tiene importancia en nuestro ejercicio.

Ahora, lo que hacemos es pintar los resultados y las gráficas quedarían como las siguientes:

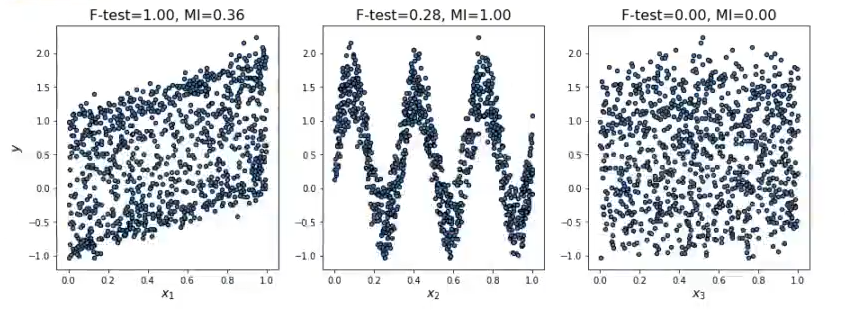
Para x₁ frente a y, que como vemos es una relación lineal, F – test nos está mostrando que es muy importante esta variable, ya que el resultado que nos muestra es F – test = 1.00. Por otro lado, para x₁ el mutual info o MI nos está dando 0.36.

Para x₂, que tenemos una relación claramente no lineal, F – test da como resultado 0.28, porque no es capaz de captar la relación no lineal, y el mutual info da como resultado 1.00, lo que significa que es demasiado alto.

Por último, con x₃ ambos métodos de filtrado para regresión lineal, tanto el F – test como el mutual_info, concuerdan en que no hay ningún tipo de relación.

Vamos a comprobar qué sucede si, en vez de 1000 datos, le ponemos 100:

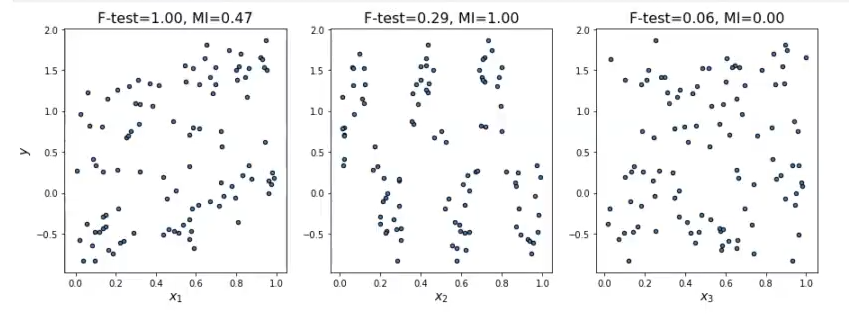
Vemos que la diferencia no es mucha e, incluso, se puede ver una relación más clara.

El Big Data es una de las disciplinas mejor pagadas y más demandadas del mercado laboral actual. Si quieres seguir aprendiendo sobre estas y otras temáticas relacionadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás toda la fundamentación teórica y práctica para incursionar en el mercado laboral y seguir cultivando tu camino hacia el éxito. ¡Anímate a cambiar tu futuro y solicita más información ahora!