Multiplicación de matrices

¿Sabías que se pueden hacer muchísimos ejercicios, entre ellos la multiplicación de matrices con arrays? En este post te hablamos sobre esto y te mostramos algunos ejercicios resueltos para que aprendas a multiplicar una matriz.

Multiplicación de matrices

Multiplicación de una matriz por un escalar

• Si r es un escalar y A es una matriz, el múltiplo escalar rA es la matriz cuyas columnas son r veces las columnas correspondientes de A.
• Al igual que con los vectores, se define -A como (-1)A y se escribe A – B en lugar de A + (-1) B.

Veamos un pequeño ejercicio de multiplicación de matrices por un escalar.

• Multipliquemos por 2 la siguiente matriz:

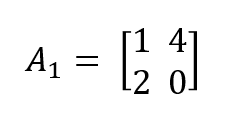
#Multiplicación de matrices
a = 2

A1 = np.array ([[1,  4], [2,  0]])
a * A1

array (

[[2, 8],
[4, 0]])

Multiplicación matricial

Si A es una matriz mxn y B es una matriz nxp con columnas b₁, b₂, … b_p, el producto AB es la matriz mxp, cuyas columnas son:

Veamos un pequeño ejercicio para entender cómo funciona la multiplicación de matrices.

• Multipliquemos las siguientes matrices:

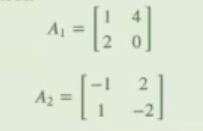
#Multiplicación de matrices
A1 = np.array ([[1,  4], [2,  0]])
A2 = np.array ([[-1,  2], [1,  -2]])

print (A1.shape)
print (A2.shape)

(2, 2)

(2, 2)

A1  * A2

array (
[[-1, 8],
[2, 0]])

No es el resultado que esperamos al hacer la multiplicación de estas matrices. El resultado debería ser algo así:

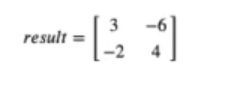
¿Por qué sucede esto?

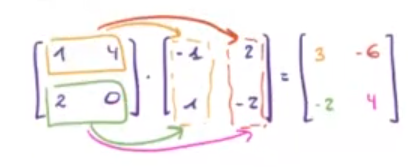
Esto se debe a que Numpy está multiplicando elemento por elemento. Esto tiene que ver más con tensores que otra cosa. Si queremos realizar la multiplicación matricial tenemos que usar np.dot ():

np.dot (A1, A2)

array (
[[3, -6],
[-2, 4]])

En general, AB ≠ BA.

Ejercicios sobre multiplicación de matrices

Veamos algunos ejercicios más para entender mejor el concepto.

• Realiza la multiplicación de AB y BA de las siguientes matrices:

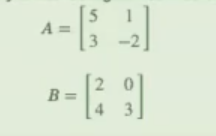
#Multiplicación de matrices
A = np.array ([[5,  1],
                         [3,  -2]])

B = np.array ([[2,  0],
                         [4,  3]])

AB = np.dot (A, B)
print (AB)

[[14 3]
[-2 -6]]

BA = np.dot (B, A)
print (BA)

[[10 2]
[29 -2]]

• Dadas las siguientes matrices A, B y C, comprueba si AB es igual a AC:

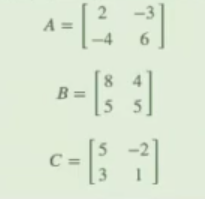
#Multiplicación de matrices
A = np.array ([[2,  -3],
                         [-4,  6]])

B = np.array ([[8,  4],
                         [5,  5]])

B = np.array ([[5,  -2],
                         [3,  1]])

#AB = np.dot (A, B)
AB = np.dot (B)
AC = np.dot (C)

Podemos usar np.array_equal () para comprobar si dos arrays son iguales:

np.array_equal (AB, AC)

True

AB

array (
[[1, -7],
[-2 14]])

AC

array (
[[1, -7],
[-2, 14]])

Ahora que sabes cómo hacer multiplicación de matrices con Numpy y np.dot, puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector. Podrás acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral en pocos meses gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!