Operaciones con tensores: división y producto tensor

En otro artículo hemos visto algunas operaciones con tensores, entre ellas la suma y el producto de tensores Hadamard. En este post, veremos cómo se lleva a cabo la división de tensores y el producto tensor. También veremos cómo trabajar tensores con TensorFlow.

Operaciones con tensores

División de tensores

La división de tensores está dada por las siguientes expresiones:

#Operaciones con tensores
A = np.array ([[[1,  2,  3], [4,  5,  6], [7,  8,  9]],
                         [[11,  12,  13], [14,  15,  16], [17,  18,  19]],
                         [[21,  22,  23], [24,  25,  26], [27,  28,  29]]])

B = np.array ([[[1,  2,  3], [4,  5,  6], [7,  8,  9]],
                         [[11,  12,  13], [14,  15,  16], [17,  18,  19]],
                         [[21,  22,  23], [24,  25,  26], [27,  28,  29]]])

C = A / B
print (C)

[[[1. 1. 1.]

[1. 1. 1.]

[1. 1. 1.]]

[[[1. 1. 1.]

[1. 1. 1.]

[1. 1. 1.]]

[[[1. 1. 1.]

[1. 1. 1.]

[1. 1. 1.]]]

print (A.shape)
print (B.shape)
print (C.shape)

(3, 3, 3)

(3, 3, 3)

(3, 3, 3)

Producto tensor

El operador del producto tensor a menudo se denota como un círculo con una pequeña x en el centro: ⦻.

Dado un tensor A con a dimensiones y un tensor B con r dimensiones, el producto de estos tensores será un nuevo tensor con q + r dimensiones.

El producto tensor no se limita a tensores, sino que también se puede realizar en matrices y vectores, que pueden ser un buen lugar para practicar con el fin de desarrollar la intuición para dimensiones superiores.

Producto tensor para vectores

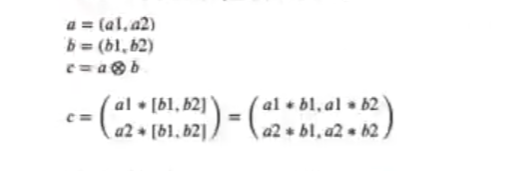
Producto tensor para matrices

Numpy puede realizar el producto tensor usando la función tensordot. La función toma como argumentos los dos tensores a multiplicar y el eje sobre el que se suman los productos, llamada sum reduction. Para calcular el producto tensor, también llamado producto de punto tensor en nympy, el eje debe establecerse en 0.

#Operaciones con tensores
A = np.array ([1,  2])
B = np.array ([3,  4])

C = np.tensordot (A, B, axes = 0)

print (C)

[[3 4]

[6 8]]

#Igual a np.dot (A, B), pero para tensores

#Operaciones con tensores
A = np.array ([[[1,  2,  3], [4,  5,  6], [7,  8,  9]],
                         [[11,  12,  13], [14,  15,  16], [17,  18,  19]],
                         [[21,  22,  23], [24,  25,  26], [27,  28,  29]]])

B = np.array ([[[1,  2,  3], [4,  5,  6], [7,  8,  9]],
                         [[11,  12,  13], [14,  15,  16], [17,  18,  19]],
                         [[21,  22,  23], [24,  25,  26], [27,  28,  29]]])


C = np.tensordot (A, B)
C.shape

(3, 3)

Tensores con TensorFlow

Entre las operaciones con tensores, vamos a ver algunos pequeños ejemplos sobre tensores usando tensorflow:

import tensorflow as tf
import numpy as np

#!pip install tensorflow

Con tf.constant () generamos une scalar tipo int32:

#Operaciones con tensores
rank_tensor = tf.constant (4)
print (rank_0_tensor)

tf.Tensor (4, shape = (), dtype = int32)

Crear un vector

También podemos crear un vector.

Con un axis (axis 1)

#Operaciones con tensores
rank_tensor = tf.constant ([2.0,  3.0,  4.0])
print (rank_1_tensor)

tf.Tensor ([2. 3. 4.], shape = (3, ), dtype = float32)

#Operaciones con tensores
rank_1_tensor.shape

TensorShape ([3])

rank_1_tensor.dtype

tf.float32

0.333152

0.333152

1

1

Con dos axis (axis 2)

#Operaciones con tensores
rank_2_tensor = tf.constant ([1,  2],
                                                   [3,  4],
                                                   [5,  6], dtype = tf.float16)

rank_2_tensor

<tf.Tensor: shape = shape = (3, 2), dtype = float16, numpy =

array ([[1., 2.],

[1., 2.],

[1., 2.]], dtype = float16)>

Con más axis

#Operaciones con tensores
rank_3_tensor = tf.constant ([[[0,  1,  2,  3,  4],
                                                      [5,  6,  7,  8,  9],
                                                    [[10,  11,  12,  13,  14],
                                                     [15,  16,  17,  18,  19],
                                                    [[20,  21,  22,  23,  24],
                                                     [25,  26,  27,  28,  29]]])

rank_3_tensor

<tf.Tensor: shape = (3, 2, 5), dtype = int32, numpy = array(

[[[0, 1, 2, 3, 4],

[5, 6, 7, 8, 9],

[[10, 11, 12, 13, 14],

[15, 16, 17, 18, 19],

[[20, 21, 22, 23, 24],

[25, 26, 27, 28, 29]]])>

Hay muchas formas de visualizar un tensor con 3 axis:

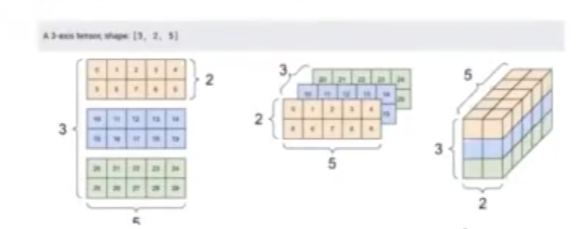
Con np.array () podemos convertir un tensor a una variable de numpy:

#Operaciones con tensores
np.array (rank_2_tensor)

type (np.array (rank_2_tensor))

numpy.ndarray

np.array (rank_2_tensor).shape

(3, 2)

También podemos realizar operaciones matemáticas como suma, resta, multiplicación o división. Incluso podemos realizar otro tipo de operaciones con tensores que son muy usadas, como son:

• tf.reduce_max () para encontrar el valor más grande.
• tf.argmax () para encontrar el índice de valor más grande.

¿Quieres seguir aprendiendo?

Si quieres seguir aprendiendo, podrás acceder a una de las disciplinas más demandadas con la guía del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación en la que adquirirás todos los conocimientos imprescindibles para obtener el trabajo de tus sueños en pocos meses. ¡Entra ya para solicitar información e impulsa tu futuro!