Operador diferencial d/dx: ¿Qué es y cómo se usa en cálculo?

El operador diferencial d/dx en cálculo se usa para analizar el cambio y la variación en matemáticas y ciencias.

Más o menos es como aprender a montar en bicicleta: al principio puede parecer confuso, pero una vez que entiendes el truco, el movimiento fluye de manera natural.

Aquí te mostraré qué es el operador diferencial d/dx, cómo se usa y algunos ejemplos prácticos que te ayudarán a dominarlo.

¿Qué es el operador diferencial d/dx?

d/dx es un operador diferencial que se utiliza en cálculo para encontrar la derivada de una función con respecto a la variable x.

En términos simples, nos ayuda a medir cómo cambia una función cuando su variable cambia ligeramente. Es como medir la pendiente de una curva en un punto específico.

• Por ejemplo, si tienes una función f(x) = x², el operador diferencial d/dx te indica cómo cambia el valor de f(x) cuando x varía mínimamente.

¿Cómo interpretar el operador diferencial d/dx?

Piensa en el operador d/dx como una lupa matemática que se enfoca en cómo cambia algo en el más mínimo detalle.

Cuando aplicas d/dx a una función, obtienes la derivada, que esencialmente mide la velocidad de cambio en un punto dado.

• Por ejemplo:

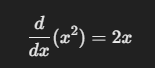
Aquí, el resultado nos dice que la pendiente de la curva x² en un punto específico es el doble del valor de x en ese punto.

Notación y simbología del operador diferencial

• El operador diferencial se expresa generalmente como:

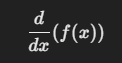
O simplemente:

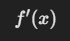
El d/dx indica la operación de derivación respecto a x, mientras que f'(x) representa el resultado de esa derivación.

Derivación paso a paso: El enfoque práctico

Veamos un ejemplo sencillo para que entiendas cómo aplicar el operador diferencial:

1. Identificar la función: Supongamos que tenemos f(x) = 3x³ + 2x² – 5x + 7.
2. Aplicar el operador d/dx a cada término:
   • La derivada de 3x³ es 9x².
   • La derivada de 2x² es 4x.
   • La derivada de -5x es -5.
   • La derivada de 7 es 0.
3. Resultado final:

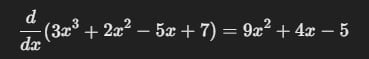
Propiedades del operador diferencial d/dx

El operador diferencial cumple con ciertas propiedades útiles:

• Linealidad: La derivada de una suma es la suma de las derivadas.
• Constantes: La derivada de una constante es 0.
• Multiplicación por constante:

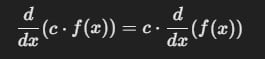
Aplicación práctica: Derivadas comunes

Aquí tienes algunas derivadas rápidas que verás frecuentemente:

• Potencia de x:

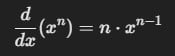
• Funciones trigonométricas:

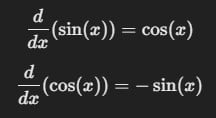
Ejemplos prácticos en programación

El operador diferencial también tiene aplicaciones en algoritmos numéricos y análisis de datos.

• Por ejemplo, en modelos de regresión lineal, calculamos derivadas para ajustar curvas.

En Python, puedes usar librerías como SymPy para derivar expresiones matemáticas de manera automática:

Imaginemos que tienes una función f(x)=2×3+3×2−5x+1 y queremos calcular su derivada con respecto a x.

Código en Python:

from sympy import symbols, diff

# Definir la variable
x = symbols('x')

# Definir la función
f = 2*x**3 + 3*x**2 - 5*x + 1

# Calcular la derivada
derivada = diff(f, x)

# Mostrar el resultado
print(f"La derivada de f(x) = 2x³ + 3x² - 5x + 1 es: {derivada}")

Resultado:

La derivada de f(x) = 2x³ + 3x² - 5x + 1 es: 6*x**2 + 6*x - 5

Explicación:

1. Símbolos: Usamos la librería SymPy para crear un símbolo matemático, en este caso, x.
2. Definición de la función: Definimos f(x)=2×3+3×2−5x+1
3. Cálculo de la derivada: Usamos la función diff() de SymPy para calcular la derivada de la función con respecto a x.
4. Resultado: El código imprime la derivada de la función: 6×2+6x−5, que es el resultado esperado según las reglas de derivación.

Domina el operador diferencial d/dx

Si el operador diferencial d/dx te parecía intimidante, ¡ya no más! Lo esencial es comprender el concepto de cambio y cómo aplicarlo a funciones concretas.

Ahora que ya conoces su importancia y aplicaciones prácticas, es el momento de seguir practicando y llevar tus habilidades al siguiente nivel.

¿Quieres aprender cálculo desde cero y aplicarlo en programación? El Bootcamp de Programación desde Cero de KeepCoding es el lugar perfecto para ti.

Te ayudaremos a adquirir habilidades prácticas que revolucionarán tu carrera profesional. ¡Atrévete a dar el paso hacia un futuro lleno de oportunidades!