¿Sabías que se puede hacer optimización con ecuaciones polinómicas? En los procesos concernientes a la función de pérdida o loss function podemos incluir un procedimiento denominado optimización con ecuaciones polinómicas.
En este post veremos de qué se trata y si, en efecto, es viable o si, por el contrario, aunque se puede hacer, es una pérdida de tiempo.
Optimización con ecuaciones polinómicas
En otro artículo hemos visto qué es la función de pérdida o loss function y en qué consiste. Pues bien, supongamos que tenemos una función de pérdida que queremos optimizar, queremos encontrar los parámetros que mejor funcionen para nuestro modelo con nuestros datos. Es decir, vamos a optimizar esta función de pérdida para obtener los mejores parámetros para nuestro modelo.
¿Cómo optimizamos la función de pérdida? Pues usando un optimizador. Uno de los optimizadores que vamos a emplear es el gradiente descendente. El término gradiente significa que es una derivada parcial respecto a las variables de la función.
¿Qué sucede con la derivada en el proceso de optimización con ecuaciones polinómicas? Lo que pasa es que en el punto en que se ha creado utilizando un valor absoluto la derivada no existe, no es derivable, es una indeterminación.
En cambio, si empleamos ecuaciones al cuadrado en vez de optimización con ecuaciones polinómicas, nos aseguramos de que toda la función sea derivable. Esto nos permite que podamos utilizar los métodos que tenemos de optimización.
Ejemplo
Veamos cómo funcionan las ecuaciones cuadráticas en lugar de la optimización con ecuaciones polinómicas por medio de un ejemplo. Imaginemos que tenemos el siguiente polinomio:
y (x) = ax2 + bx + c
Esta función está escrita sobre la base de x, es decir, solo le introducimos un valor y nos va a dar otro valor.
Veamos:
y (x) = 2x2 + x + 1
En este caso, b sería 1. Si esta función la evaluamos usando:
- y (x = 0) esto nos debería dar 1 → y (x = 0) = 1
- y (x = 1) esto nos daría 4
- y (x = -1) = 2
Si seguimos evaluando esto, lo cual podemos hacer con Python, la forma que nos daría sería la siguiente, es una parábola:
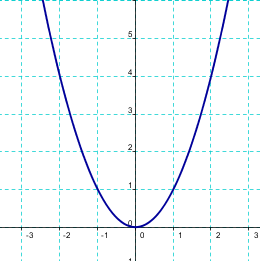
Si tenemos, en vez de lo anterior, una ecuación como esta (un valor absoluto):
y (x) = l ax + b l
Veamos cómo se comporta si lo reemplazamos:
y (x) = l 2x + 1 l
- y (x = 0) = 1
- y (x = -1) = l -1 l = 1
- y (x = -2) = l -3 l = 3
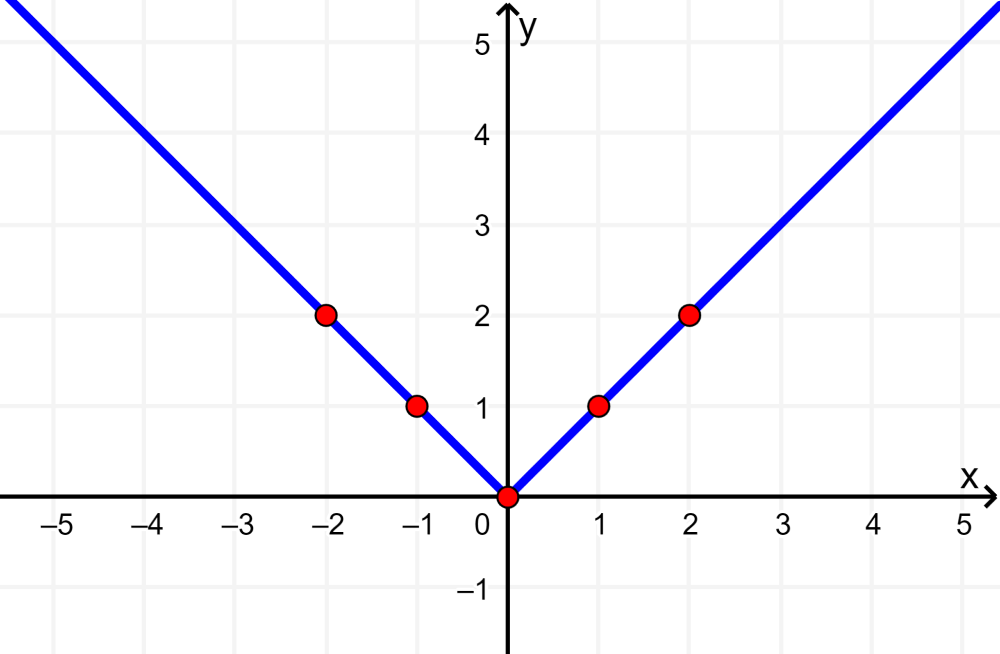
¿Qué sucede con esto? Pues que todos los valores negativos van a ser positivos porque todo lo que esté en valor absoluto y sea negativo pasa a ser positivo. Asimismo, todos los valores positivos van a seguir siendo positivos, se van a quedar igual.
Entonces, si tenemos los ejes x e y, todos los valores menores que 0 (x < 0) van a ser positivos y todos los valores mayores que 0 (x > 0) van a seguir siendo positivos. Esto quiere decir que no tendremos ningún punto negativo, por tanto, el punto de unión de la ecuación (el medio) graficada no es derivable, porque no existe tal derivada ahí.
El Big Data es una de las áreas en las que más trabajos se ofertan. Si te gustaría acceder a este tipo de opciones laborales, es el momento de seguir aprendiendo sobre optimización con ecuaciones polinómicas y cuadráticas. Esto y mucho más lo tenemos en el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños. ¡No esperes más para seguir tu camino hacia el éxito y solicita más información ahora!











