¿Sabías que se puede predecir la dureza del hormigón con R? En este artículo te mostraremos un ejercicio de aplicación en el que podremos predecir la dureza del hormigón con R, algo que puede ser de suma utilidad en la ingeniería civil.
Predecir la dureza del hormigón con R
El hormigón es el material más importante en la ingeniería civil. La resistencia a la compresión del hormigón es una función altamente no lineal de la edad y los ingredientes.
Características de los datos
Para predecir la dureza del hormigón con R es necesario saber las características de los datos.
La resistencia a la compresión real del hormigón (MPa) para una mezcla dada bajo una edad especifica (días) se determinó a partir del laboratorio. Los datos están en forma cruda (no a escala).
Resumen estadístico
En el ejercicio de predecir la dureza del hormigón con R se presenta un resumen estadístico.
Número de instancias (observaciones): 1030
Cantidad de Atributos: 9
Desglose de atributos: 8 variables de entrada cuantitativas y 1 variable de salida cuantitativa
Faltan valores de atributo: ninguno
- Cemento (componente 1) – cuantitativo – kg en una mezcla m3 – Variable de entrada.
- Escoria de alto horno (componente 2) – cuantitativa – kg en una mezcla de m3 – Variable de entrada.
- Cenizas volantes (componente 3) – cuantitativo – kg en una mezcla m3 – Variable de entrada.
- Agua (componente 4) – cuantitativa – kg en una mezcla m3 – Variable de entrada.
- Superplastificante (componente 5) – cuantitativo – kg en una mezcla m3 – Variable de entrada.
- Agregado grueso (componente 6) – cuantitativo – kg en una mezcla m3 – Variable de entrada.
- Agregado fino (componente 7) – cuantitativo – kg en una mezcla m3 – Variable de entrada.
- Edad cuantitativa – Día (1~365) – Variable de entrada.
- Resistencia a la compresión del hormigón – cuantitativa – MPa -Variable de salida.
In [ ] : concrete <- read.csv ("data/Concrete_Data.csv",
col.names = c ("cemento", "escoria", "cenizas", "agua", "plastificante", "aggrueso", "agfino", "edad", "res")
head (concrete)| cemento | escoria | cenizas | agua | plastificante | aggrueso | agfino | edad | resistencia | |
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 540.0 | 0.0 | 0 | 162 | 2.5 | 1040.0 | 676.0 | 28 | 79.99 |
| 2 | 540.0 | 0.0 | 0 | 162 | 2.5 | 1055.0 | 676.0 | 28 | 61.89 |
| 3 | 332.5 | 142.5 | 0 | 228 | 0.0 | 932.0 | 594.0 | 270 | 40.27 |
| 4 | 332.5 | 142.5 | 0 | 228 | 0.0 | 932.0 | 594.0 | 365 | 41.05 |
| 5 | 198.6 | 132..4 | 0 | 192 | 0.0 | 978.4 | 825.5 | 360 | 44.30 |
| 6 | 266.0 | 114.0 | 0 | 228 | 0.0 | 932.0 | 670.0 | 90 | 47.03 |
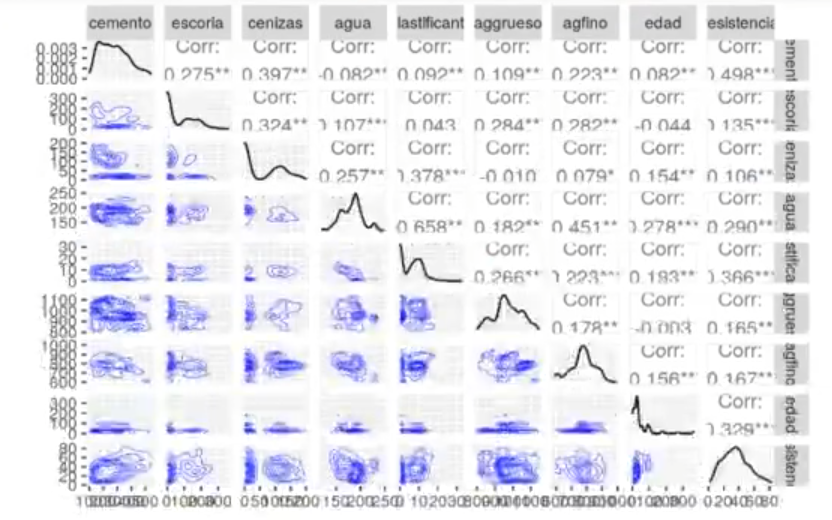
In [ ] : ggpairs(concrete,
lower = list (continuous = wrap ("density", alpha = 0.8, size = 0.2, color = "blue'))
#lower = list (continuous = wrap ("points, alpha = 0.3, size = 0. 1, color = 'blue'))
)
In [87]: set.seed(12)
idx <- sample (1:nrow (concrete), nrow (concrete) * 0.7)
train.df <- concrete [idx,]
test.df <- concrete [-idx,]
In [91]: model <- lm (resistencia ~.~ agfino - jaggrueso, train.df) summary (model)Call:
lm (formula = resistencia ~ . ~ agfino – aggrueso, data = train.df)
Residuals:
Min: -28.723
1Q: -6.407
Median: 0.920
3Q: 6.713
Max: 32.034
Coefficients:
| Estimate | Std. | Error | t value | Pr (> ltl) | |
| (Intercept) | 29.672386 | 4. | 948951 | 5.996 | 3.22e – 09 *** |
| cemento | 0.108210 | 0. | 005001 | 21.638 | < 2e – 16 *** |
| escoria | 0.088363 | 0. | 005923 | 14.918 | < 2e – 16 *** |
| cenizas | 0.071747 | 0. | 009023 | 7.951 | 7.21e – 15 *** |
| agua | 0.226535 | 0. | 024983 | -9.068 | < 2e – 16 *** |
| plastificante | 0.222432 | 0. | 099599 | 2.233 | 0.0258 * |
| edad | 0.112676 | 0. | 006341 | 17.769 | < 2e – 16 *** |
Residual standard error: 10.5 on 714 degrees of freedom
Multiple R-squared: 0.6294
Adjusted R-squared: 0.6263
F-statistic: 202.1 on 6 and 714 DF, p-value: < 2.2e – 16
In [94]: paste ("R^2 testing:", myrsquared (test.df$resistencia, predict (model, test.df)))
plot (train.df$resistencia, train.df$resistencia - predict (model, train.df))
plot (test.df$resistencia, test.df$resistencia - predict (model, test.df))
hist (test.df$resistencia - predict (model, test.df))‘R^2 testing: 0.564544320934332
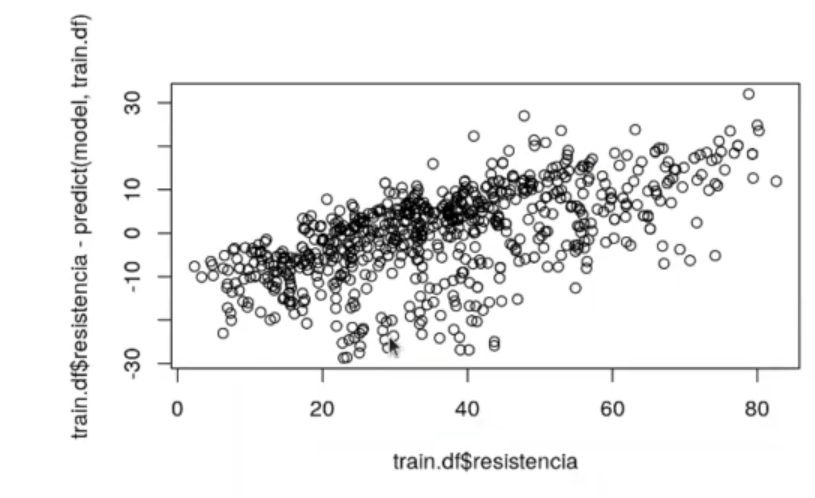
Siguiendo con el ejercicio de predecir la dureza del hormigón con R, en este punto, en el que se muestra la tendencia del modelo, es donde empezamos a ver problemas con el mismo.
El R^2 testing es más bajo que el training (0.6294), con lo cual se intuye que el modelo no está generalizando bien.
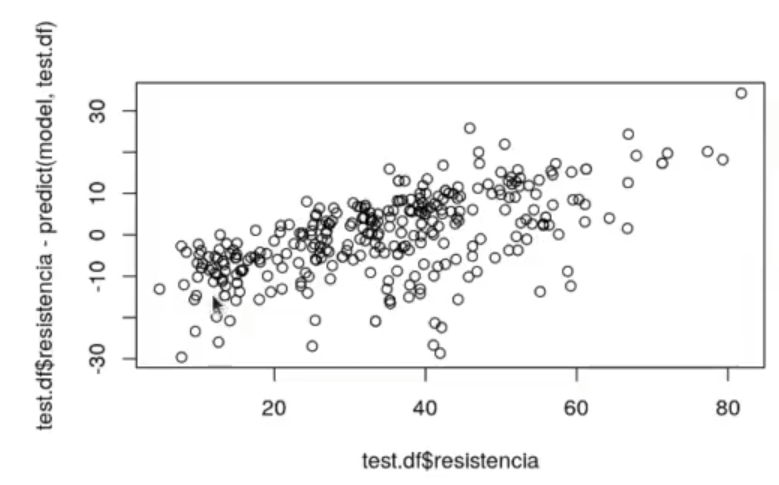
Tanto para el training como para el test se observa la misma tendencia.
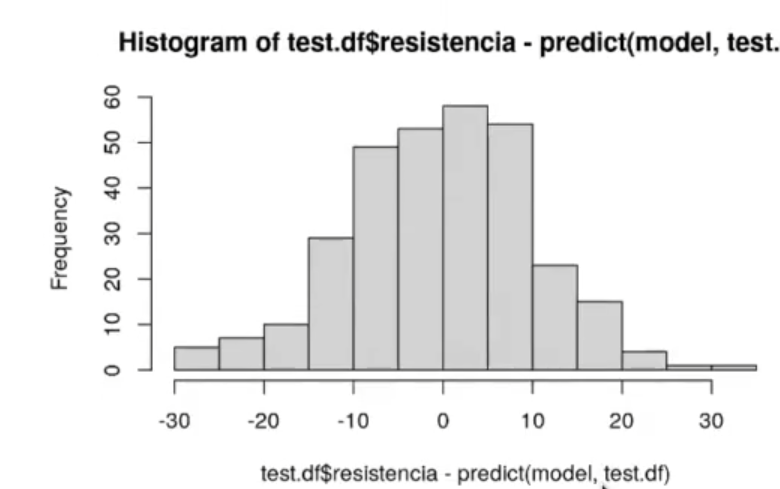
Los resultados del histograma en el ejercicio de predecir la dureza del hormigón con R muestran que los residuos, al principio, tienen una tendencia gaussiana. No obstante, en las representaciones del testing y el training, se está perdiendo mucho, ya que no se observan patrones.
Una de las formas en las que se puede corregir esto es aumentar el grado del polinomio y calcular con distintos valores, cómo sería para distintos grados de distintos polinomios y combinaciones entre training y test. La gráfica quedaría así:
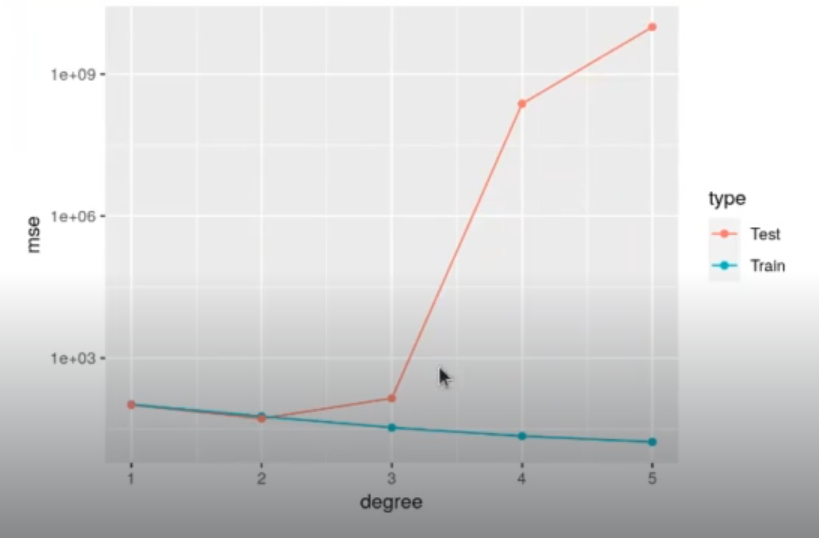
Observamos que, al parecer, el óptimo está en dos, ya que a partir de este número empiezan a darse discrepancias y los grados fluctúan bastante.
Con esto ya tenemos terminado el ejercicio de predecir la dureza del hormigón en R.
El ejercicio de aplicación acerca de predecir la dureza del hormigón con R puede parecer difícil, por eso, si necesitas ayuda en este camino de aprendizaje, recuerda que en Keepcoding tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación intensiva aprenderás en poco tiempo todo lo necesario para incursionar en un mercado laboral lleno de oportunidades. ¡Anímate a pedir información!











