El día de hoy te vamos a enseñar a identificar problemas lineal y no linealmente separables por medio de un ejercicio de aplicación.

Problemas lineal y no linealmente separables

Linealmente separable

Lo primero que haremos para determinar cuáles son los problemas lineal y no linealmente separables es representar:

#Problemas lineal y no linealmente separables
plt.scatter (ejemplo1 [ 'x1' ], ejemplo1 [ 'x2'], c = ejemplo1 [ 'label' ], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
plt.show ()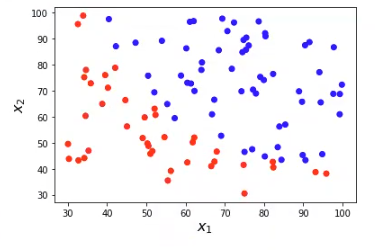

Se dice que este problema es linealmente separable, porque podemos trazar una recta para separar (no de forma perfecta) las dos clases (representadas en distintos colores, rojo y azul).

En el plano bidimensional: recta
En un espacio n-dimensional: hiperplano

No linealmente separable

#Problemas lineal y no linealmente separables
ejemplo2 = pd.read_csv ("./data/ex2data.txt", sep = " , ", header =  None, names = ['x1', 'x2', 'label'])

plt.scatter (ejemplo2 ['x1'], ejemplo2 ['x2'], c = ejemplo2 ['label'], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)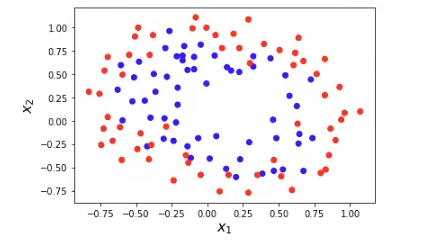

Se dice que este problema es no linealmente separable, porque no podemos trazar una recta para separar las dos clases (representadas en distintos colores, rojo y azul).

¿Lineal o no linealmente separable?

Ahora que has visto ejemplos de ambos problemas lineal y no linealmente separables, ¿qué te parece si adivinas el próximo ejercicio?:

#Problemas lineal y no linealmente separables
# Ejemplo 3: Problema XOR
np.random.seed (0)

#parameters
N = 800
mu = 1.5     # Cambia este valor
sigma = 1   # Cambia este valor

#variables auxiliares
unos = np.ones (int (N / 4))
random4 = sigma * np.random.randn (int (N / 4),1)
random2 = sigma * np.random.randn (int (N / 2),1)

#features
y3 = np.concatenate ([ -1 * unos,     unos,     unos,     -1 * unos])
X1= np.concatenate ([-mu + random4,   -mu + random4, mu + random4])
X2 = np.concatenate ([ + mu + random2,     -mu + random2])
X3= np.hstack ((X1, X2))

plt.scatter (X3 [ : , 0], X3 ([ , 1] , c = y3, cmap = cm_bright)
plt.xlabel("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
plt.show ()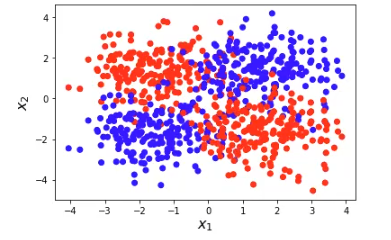

Este ejemplo no viene de datos, sino que lo estamos fabricando.

Generamos una serie de arrays auxiliares, un array de unos, también generamos un random y luego lo que hacemos es concatenar.

Pausa activa para que pienses si el problema está separado linealmente o no…

Al igual que en el caso anterior, este ejemplo tampoco es linealmente separable, y se conoce como problema XOR. La ventaja del problema XOR es que conocemos cuál es la separación óptima a priori:

Clase 1, color azul: x₁, x₂ > 0, y x₁, x₂ <0 (cuadrantes 2 y 3)
Clase 2, color rojo: x₁ < 0, x₂ > 0, y x₁ > 0, x₂ < 0 (cuadrantes 1 y 4)

Sabemos que, si x₁ y x₂ es mayor que cero, o bien, si x₁ y x₂ es menor que cero, tenemos los cuadrantes azules (dos y tres).

En cambio, si una es menor que cero y la otra es mayor, en cualquiera de los dos sentidos, tenemos los cuadrantes rojos (uno y cuatro).

De los tres ejemplos que vimos, ninguno tiene fronteras perfectas. El ejemplo 1, en donde se ve con claridad que existe un problema linealmente separable, hay pequeños datos o grupos de datos que interfieren con la línea recta (si estuviéramos hablando de una gráfica en dos dimensiones).

En el ejemplo 2, pese a ser no linealmente separable, se puede ver con claridad una especie de separación, aunque no pueda crearse una recta con dicha separación; pese a esto, la línea tampoco es muy clara, ya que algunos datos se cruzan entre sí e impiden la separación directa.

En el ejemplo 3, denominado problema XOR, también se puede observar que existen distintos grupos de datos (grupo azul, conformado por los cuadrantes 2 y 3; y grupo rojo, conformado por los cuadrantes 1 y 4), no obstante, si quisiéramos representar la separación de estos grupos con una línea recta en un plano bidimensional, no sería posible porque todos estos grupos están separados de tal forma que esta intención sea imposible.

Sean cuales sean los problemas lineal y no linealmente separables, vemos que hay una clara distinción en los diferentes grupos de datos, que no están desorganizados y puestos de manera aleatoria, sino que hay patrones, lo que nos permite diferenciar, a simple vista, distintos conjuntos de datos.

¿Qué sigue?

Ahora que hemos visto cómo diferenciar problemas lineal y no linealmente separables, podemos dar el siguiente paso y continuar aprendiendo.

Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que aprenderás todos los conocimientos teóricos y prácticos necesarios para llevar a cabo tus objetivos de convertirte en un gran programador y analista de datos.

¡Anímate a cambiar tu futuro y solicita más información!