Propiedades de la radicación y su uso en programación

La radicación, una operación matemática inversa a la potenciación, desempeña un papel crucial tanto en las matemáticas como en la programación. Conocer las propiedades de la radicación y su aplicación en algoritmos puede enriquecer nuestra comprensión de los conceptos fundamentales y ampliar nuestras capacidades en el ámbito de la programación. En este artículo, exploraremos detalladamente las propiedades de la radicación y cómo estas influyen en el desarrollo de programas informáticos.

¿Qué es la radicación?

La radicación, en el ámbito matemático, representa una operación fundamental que se utiliza como la inversa de la potenciación. Mientras que la potenciación implica elevar un número a una potencia determinada, la radicación busca encontrar el número raíz, es decir, el valor que, elevado a una cierta potencia, produce el número original. Por ejemplo, la raíz cuadrada de 25 es 5, porque 5 elevado al cuadrado resulta en 25. Este concepto es fundamental en diversas ramas de las matemáticas y tiene aplicaciones prácticas en la resolución de problemas de ingeniería, física y otras disciplinas científicas.

Cuando hablamos de la raíz, nos referimos al número que, elevado a una cierta potencia, produce el número original. Por ejemplo, la raíz cuadrada de 25 es 5 porque 5^2 = 25. De manera similar, la raíz cúbica de 8 es 2, ya que 2^3 = 8. Esta noción es esencial para comprender cómo funciona la radicación y su aplicación en diversas situaciones matemáticas y prácticas.

La radicación se expresa mediante un símbolo específico, que incluye el índice, el radicando y la raíz. El índice indica la cantidad de veces que el número raíz se multiplica por sí mismo para obtener el radicando. Si no se especifica ningún número, por defecto el índice es 2. Por ejemplo, la raíz cuadrada de un número se representa con el símbolo √, mientras que la raíz cúbica se representa con el símbolo ∛. Esta notación proporciona una forma clara y concisa de expresar operaciones de radicación en términos matemáticos.

Propiedades de la radicación

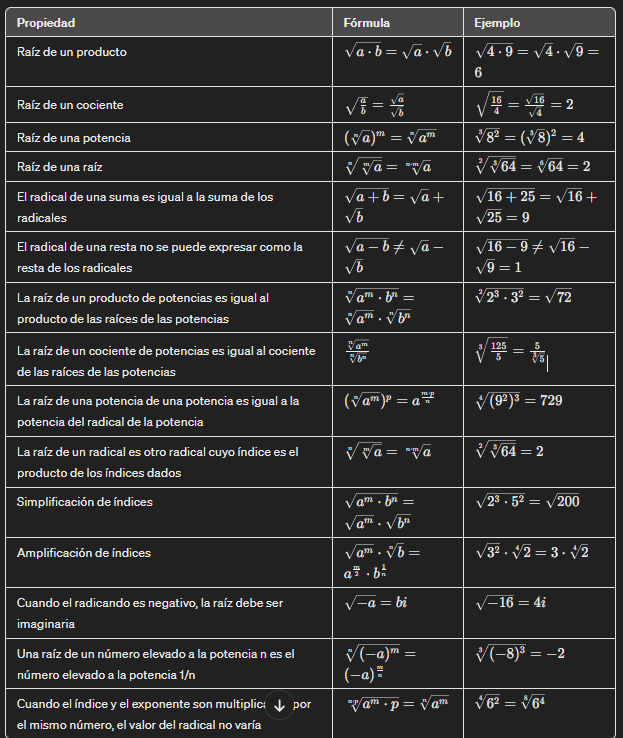
Existen unas propiedades de la radicación que son fundamentales, veamos cuáles son:

1. Radicación de un producto:
   Esta propiedad nos permite separar la raíz de un producto en dos raíces individuales. Matemáticamente, se expresa como “la raíz n-ésima de (a * b) es igual a la raíz n-ésima de a multiplicada por la raíz n-ésima de b”.
2. Radicación de un cociente:
   En esta propiedad, dividimos la raíz de un cociente en dos raíces separadas. Matemáticamente, se representa como “la raíz n-ésima de (a / b) es igual a la raíz n-ésima de a dividida por la raíz n-ésima de b”.
3. Radicación de una potencia:
   Permite encontrar la raíz de una potencia. Si tenemos “la raíz n-ésima de (a^m)”, esta propiedad nos dice que es equivalente a “a elevado a la potencia m dividido por n”.
4. Radicación de una raíz:
   Nos permite combinar raíces. Si tenemos “la raíz m-ésima de la raíz n-ésima de a”, podemos expresarlo como “la raíz m * n-ésima de a”.

Existen otras propiedades menos frecuentes o más específicas que también se pueden estudiar en contextos particulares. Algunas de estas propiedades adicionales pueden incluir:

1. Radicación de un exponente negativo: Permite manejar casos donde el exponente dentro de la raíz es negativo, generalmente transformándolos en fracciones.
2. Radicación de una suma o resta: Es posible aplicar la radicación a expresiones que involucran sumas o restas de radicandos.
3. Radicación de potencias fraccionarias: Hace alusión a la radicación de expresiones donde el radicando es una potencia con exponente fraccionario.
4. Radicación de números complejos: Las propiedades de la radicación también pueden extenderse para incluir números complejos.
5. Radicación de un cuadrado perfecto: La raíz de un cuadrado perfecto es exacta y puede ser un número entero.
6. Radicación de un cubo perfecto: Similar a los cuadrados perfectos, los cubos perfectos tienen raíces exactas.
7. Radicación de un radicando negativo: En algunos casos, es posible manejar radicandos negativos dependiendo del índice de la raíz.
8. Radicación de expresiones racionales: La radicación puede aplicarse a expresiones racionales para simplificarlas o resolverlas.
9. Radicación de funciones trigonométricas: En contextos más avanzados, la radicación puede aplicarse a funciones trigonométricas para resolver ecuaciones.
10. Radicación de polinomios: La radicación puede involucrar polinomios, especialmente en el contexto de encontrar raíces de ecuaciones polinómicas.
11. Radicación de matrices y determinantes: En álgebra lineal, la radicación puede aplicarse a matrices y determinantes en ciertos casos.

Veamos algunos ejemplos de cada una de estas propiedades de la radicación:

Aplicación en programación

En programación, las propiedades de la radicación se utilizan en una variedad de situaciones, desde cálculos matemáticos hasta la implementación de algoritmos complejos y matemáticas para la ciencia de datos. Por ejemplo, en algoritmos de búsqueda o en la manipulación de estructuras de datos, entender cómo calcular rápidamente raíces cuadradas o cúbicas puede ser esencial para optimizar el rendimiento del programa. Esto lo puedes hacer con lenguajes como Python, que presentan diferentes herramientas encaminadas a resolver operaciones matemáticas en ciencia de datos.

Dominar conceptos matemáticos como las propiedades de la radicación es crucial para sobresalir en el campo de la programación. En el Bootcamp de programación desde cero que tenemos en KeepCoding, no solo aprenderás los fundamentos de la programación, sino también las operaciones matemáticas con Python, necesarias para enfrentar desafíos complejos en el mundo real. ¡Únete a nosotros y hazte un experto en tecnología!