¿Sabes en qué consiste la pseudoinversa Moore-Penrose? En este artículo te lo contamos.
Pseudoinversa Moore-Penrose: contextualización
Supongamos que tenemos un modelo de regresión lineal simple que convertimos en una matriz. ¿Qué ocurre si la matriz que queremos invertir no es cuadrada? El sistema de ecuaciones no tendría una única solución o, simplemente, no tendría solución.
Tenemos la siguiente función de regresión lineal simple:
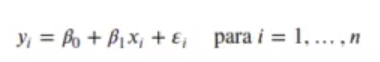
Esta función la expandimos del siguiente modo:
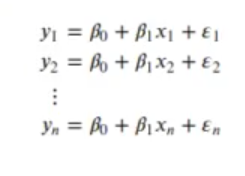
Donde:
- yi: i-ésimo valor de la variable dependiente.
- xi: i-ésimo valor de la variable independiente.
- B0.B1: parámetros a determinar que un dato conjunto de xi produce los mejores yi.
- B0: puede llamarse sesgo, bias, intercept o término constante. Indica el corte en el eje Y.
- B1: puede llamarse pendiente o slope. Indica cuánto aumenta Y por cada incremento de X.
- Ei: error, valor aleatorio.
La matriz quedaría así:
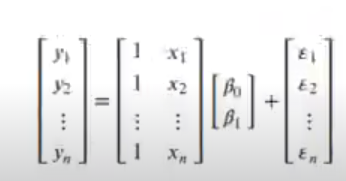
Lo que se puede simplificar como:
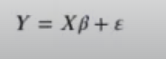
Donde:
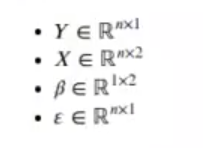
Podemos usar la matriz inversa para resolver ecuaciones:
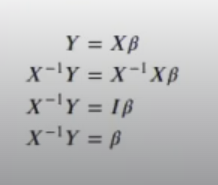
O podemos usar la pseudoinversa Moore-Penrose para minimizar el error cuadrático medio.
Para números reales se define como:
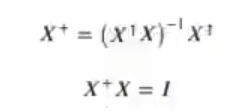
El problema original consistía en querer calcular ẞ de tal forma que se minimice la influencia de E:
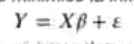
En nuestro sistema es desconocido, pero sabemos que tiene una media de cero y varianza finita. Así que simplificamos el siguiente sistema de ecuaciones:
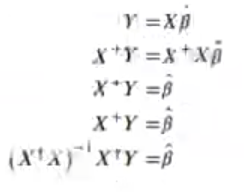
Ahora, tenemos a partir de X e Y una estimación. Podemos, a partir de valores conocidos de X, calcular una estimación de Y.
Evidentemente:
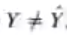
Llamaremos residuo (error) a la diferencia entre el valor real y el valor estimado.
El método anterior garantiza que el error cuadrático medio sea mínimo:
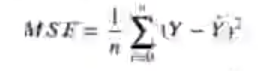
Es decir, nuestra tarea consiste en minimizar la función MSE para que nuestro modelo Y sea óptimo. La función MSE es convexa y cuadrática.
La pseudoinversa Moore-Penrose sirve para minimizar el error cuadrático medio. Al final, para explicarlo y para entender cómo funciona, existe un gran inconveniente: los programas no funcionan con pseudoinversa, funcionan minimizando el error cuadrático medio.
El resultado es el mismo, pero calcular la pseudoinversa es difícil y puede darte unos valores altos, incluso infinitos.
No obstante, es importante aprender sobre todos los modos de proceder respecto a la resolución de problemas relacionados con el Big Data. Por eso, te invitamos a unirte a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el que abordaremos todas las temáticas necesarias para que, en poco tiempo, puedas destacar en el mercado laboral. ¡Te esperamos!











