El compromiso sesgo-varianza es un principio que nos permite analizar el alcance de las prestaciones (error de generalización) en tareas de aprendizaje supervisado. A continuación, detallamos cómo funciona.
¿Cómo funciona el compromiso sesgo-varianza?
Expliquemos el funcionamiento del compromiso sesgo-varianza con la siguiente imagen:
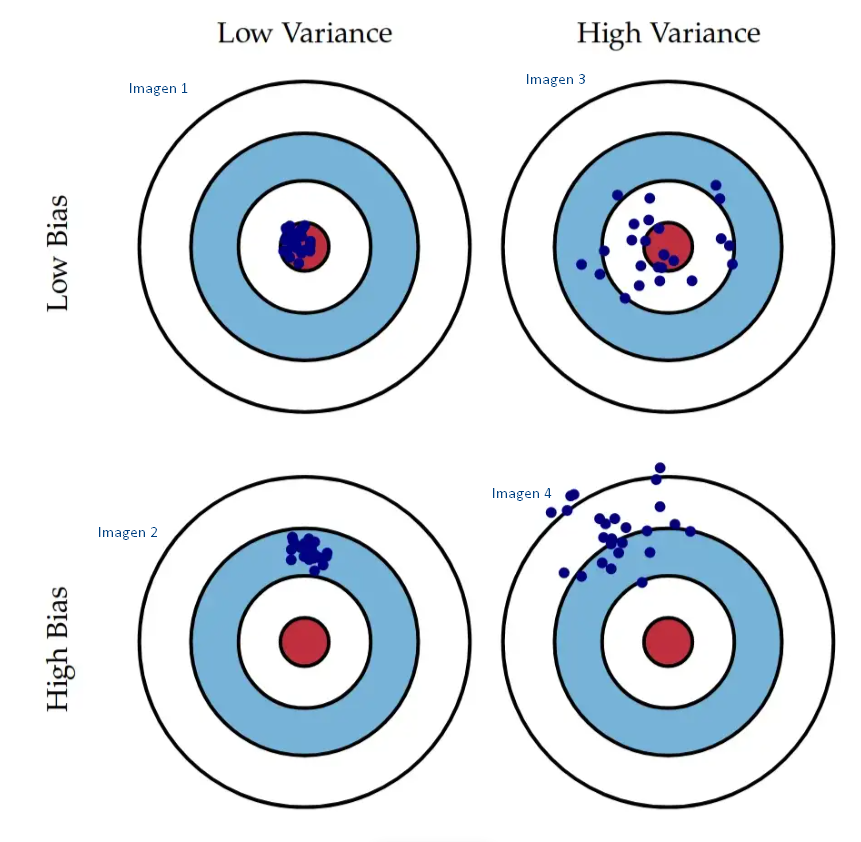
Tenemos un conjunto de datos representados en la imagen total. El compromiso sesgo-varianza que tiene un modelo está básicamente representado allí.
- Si tenemos poco sesgo y poca varianza, vamos a conseguir algo similar a lo que se presenta en el primer grupo de datos (imagen 1). Es decir, cada vez que se ingresen nuevos datos de entrenamiento, estos se van a alojar en el lugar indicado.
- Si tenemos un modelo con poca varianza y mucho sesgo, lo que resulta es un conjunto de datos similar al de la segunda imagen. Van a estar todos los datos juntos, porque tiene poca varianza; pero, al mismo tiempo, como tiene mucho sesgo, va a estar mal dentro del compromiso sesgo-varianza, porque van a estar todos juntos dentro de un lugar alejado del que queremos que estén.
- Si tenemos poco sesgo, pero mucha varianza, los datos van a estar más o menos apuntando al centro, pero muy separados entre sí; algunos caerán dentro y otros caerán fuera (imagen 3).
- Si, por último, tenemos alto sesgo y alta varianza, además de estar muy separados los datos, van a estar alejados del centro (imagen 4).
Podríamos pensar que la solución más simple para este problema es crear modelos estadísticos con sesgo y varianza bajos, pero no es tan fácil esto del compromiso sesgo-varianza, pues sucede que, cuando bajamos el sesgo de un modelo, estamos aumentando la varianza y viceversa. Es decir, manualmente no es posible tener un compromiso sesgo-varianza muy óptimo.
¿Cómo solucionar el problema del compromiso sesgo-varianza?
Supongamos que tenemos un proceso y = g (x) + ε, donde ε representa una fuente de error irreducible (ruido en los datos); esto significa que ε no se puede modificar. Tenemos, por ejemplo, datos mal tomados, personas que han saboteado la encuesta de manera intencional, datos corruptos… Son un montón de factores sobre los que nosotros no tenemos control.
Del proceso y, tenemos información de un conjunto de muestras.
D = {x(i) , y(i)}, con i = 1, … , N.
Recordemos que x es un vector e y un escalar.
A partir de estos datos D, buscamos encontrar la función fw(x) que mejor se ajuste a la verdadera función g(x), utilizando un algoritmo de machine learning.
Si supiéramos previamente el valor de g(x), no necesitaríamos machine learning, pero como no lo sabemos, necesitamos encontrar, con base en los datos D = {x(i) , y(i)}, con i = 1, … , N, que sabemos que siguen la función y = g (x) + ε, una función que sea la que más se acerque a la real.
Por mejor ajuste se entiende que se quiere medir el error cuadrático medio (y – fw(x))2, tanto para el conjunto D como para cualquier muestra no contenida en D, es decir, para instancias nuevas que ingresen en el conjunto de datos (capacidad de generalización).
Dado que y es un proceso que contiene ruido, es difícil que podamos ajustar fw(x) a g(x) de forma perfecta. Se puede demostrar que, en promedio, el error que se comete para cualquier valor de x ∉ D (error de generalización) se descompone en:
error (x) = E [ (y – fw(x) )2] = Bias [ fw(x) ]2 + Var [fw(x)] + σ²
Donde:
- Bias [ fw(x) ]2 = E [fw(x)]2 – g(x) representa el error asociado a la simplicidad del modelo.
- Var [fw(x)] representa la variabilidad del modelo frente a distintos conjuntos de entrenamiento. Pequeños cambios en el conjunto de entrenamiento pueden producir grandes errores.
- σ² es una cota al error mínimo que puedes alcanzar.
Por tanto, el objetivo es buscar un algoritmo que proporcione mínimo sesgo y mínima varianza.
¿Quieres saber más?
El compromiso sesgo-varianza es uno de los principios básicos para elegir el algoritmo adecuado en ML. Si quieres seguir aprendiendo sobre este y otros temas del Big Data, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que podrás hacer un recorrido teórico y práctico por este interesante mundillo. En cuestión de meses, podrás aprender todos los conocimientos necesarios para incursionar en uno de los mercados laborales mejor pagados en la actualidad. ¡Entra y solicita más información!







