El criterio de información de Akaike (AIC) o aic bic es un estimador de la calidad relativa del modelo que tiene en cuenta su complejidad.
A medida que se va aumentando el número de parámetros de entrada o de grados de un polinomio, el valor de R va a ser mejor, porque el error cuadrático medio disminuye. El criterio de información Akaike (aic metric) penaliza los modelos complejos en favor del los sencillos para evitar el sobreajuste.
¿Cómo se calcula el criterio de información Akaike?
Se calcula a partir del log-likelihood, el logaritmo del estimador de máxima verosimilitud:
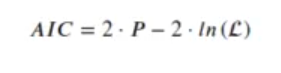
En el caso de una regresión lineal:
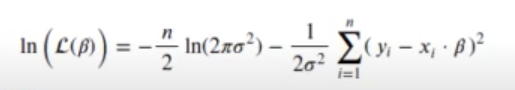
Una vez que el modelo está entrenado, resulta que:
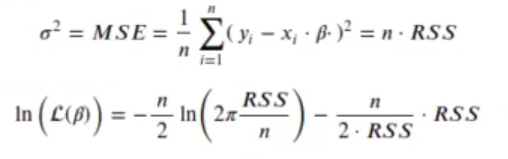
Si sustituimos en la ecuación de criterio de información akaike:
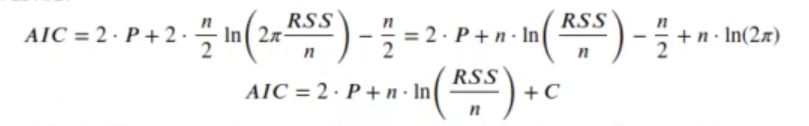
Como el valor del criterio de información Akaike realmente solo se utiliza para comparar un modelo con otro, el termino constante C se puede ignorar, porque no cambia entre los modelos.
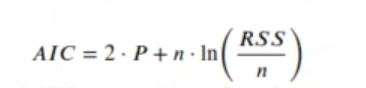
El valor P es el número de coeficientes del modelo más 1. El criterio de información Akaike suele multiplicar P por 2, pero otros valores son posibles en función de la importancia que queramos darle a los parámetros extra.
Tanto la primera como la última de las fórmulas que aparecen en las imágenes funcionan del mismo modo, es decir, el resultado de una operación hecha con una u otra no va a variar.
Cuanto más bajo sea el criterio de información Akaike, mejor.
Veamos:
// akaike info criterion
In [13] : k_val = 2
AIC (model, k = k_val)440.181501249111
In [14] : rss <- sum ((model$residuals) ^ 2)
n <- nrow (df)
// criterios de información akaike y bayesiano
In [17] : loglik <- -n / 2 * log (2 * pi * rss / n) -n / 2
In [18] : -2 * loglik + k_val * (length (model$coefficients) + 1)440.181501249111
Vemos que ambos resultados de distintas fórmulas terminan siendo los mismos.
// aic bic interpretation
In [19] : model$coefficients(Intercept): 3.6456315740211 x: 5.06324797293581
In [20] : model_lin <- lm (data = df, formula = y ~ 1)
summary (model_lin)Call:
lm (formula = y ~ 1, data = df)
Residuals:
Min: -64.14
1Q: -27.69
Median: 4.38
3Q: 24.76
Max: 65.66
Coefficients:
| Estimate | Std. Error | t value | Pr (> ltl) | |
| (Intercept) | 4.490 | 4.453 | 1.008 | 0.318 |
Residual standard error: 34.5 on 59 degrees of freedom.
En anteriores ejercicios habíamos estado usando el lm. En este caso, usamos el glm, que significa «modelo lineal generalizado», y family = gaussian. Esta fórmula es igual a:
model <- lm (data = df, formula = y ~ x)
Si se van a hacer regresiones lineales, lo mejor es usar este modelo, ya que las respuestas van a ser más rápidas y consume menos memoria, entre otros muchos beneficios.
Si usamos en la fórmula y ~ 1 en vez de y ~ 0, el intercept cambiará y, por tanto, la gráfica quedaría distinta. De modo que, si no le damos un valor a ese intercept, vamos a obtener una gráfica sin pendientes y el valor que se obtenga será la media.
In [21] : AIC (model_lin)598.166654240199
Esto también tiene un modelo más alto, por lo que vemos que la calidad es malísima.
In [22] : rss <- sum ((model_lin$residuals) ^ 2)
n <- nrow(df)
loglik <- - n / 2 * log (2 * pi * rss / n) - n / 2
- 2 loglik + 2 * (length (model_lin$coefficients) + 1)598.166654240199
In [23] : length (model_lin$coefficients)1
Hemos aprendido qué es el criterio de información Akaike o AIC y cómo funciona en modelos que son lineales y que no lo son. En ambos casos se aplica la fórmula de manera distinta, dependiendo de las necesidades de información.
Si quieres seguir aprendiendo sobre este tema, puedes inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que en muy poco tiempo podrás convertirte en un gran data scientist y conseguir el trabajo de tus sueños. ¡Anímate a solicitar más información!











