El determinante de una matriz es una medida de la distorsión que genera una transformación lineal. Aunque en un primer momento puede parecer que esta es una definición un poco vaga acerca de lo que es el determinante de una matriz, enseguida veremos que es mucho más precisa de lo que esperábamos.
¿Qué es el determinante de una matriz?
Veamos cómo funciona o de dónde se saca el determinante de una matriz.
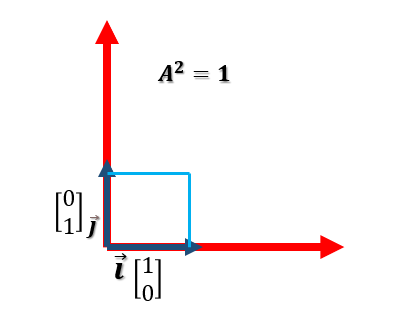
Tenemos un eje de coordenadas x e y. Asimismo, dentro de este eje se encuentran los vectores unitarios i, que corresponden al eje x, y j, que corresponden al eje y. El área de estos vectores es igual a 1.
La matriz del vector unitario i es [1/0]; la matriz del vector unitario j es [0/1]. El área de los vectores unitarios resulta de la multiplicación de ambas matrices, de modo que:
A2 = 1
¿Qué sucede si ahora le realizamos a estos vectores la siguiente transformación lineal?
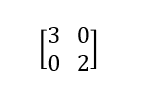
Ya sabemos que la primera columna [3/0] indica el punto en el que acaba el eje x y la segunda columna [0/2] indica dónde acaba el eje y.
Entonces, lo siguiente que haremos será desarrollar el vector x, es decir, [1/0]. Ya hemos visto que podemos hacerlo de forma matricial o de esta forma: 3x + 0y / 0x + 2y. Cancelamos los ceros, de modo que nos queda 3x / 2y. El siguiente paso es sustituir:
3 . 1 / 2 . 0 = [3 / 0]
[3/0] sería el vector resultante después de hacerle la transformación a la matriz.
Ahora desarrollaremos el vector y, que quedaría como 3x / 2y. El resultado de esto con la sustitución sería:
3 . 0 / 2 . 1 = [0 / 2]
Aquí lo que hemos hecho es la transformación lineal de ambos vectores. Entonces, si representamos estos dos vectores, quedarían así:
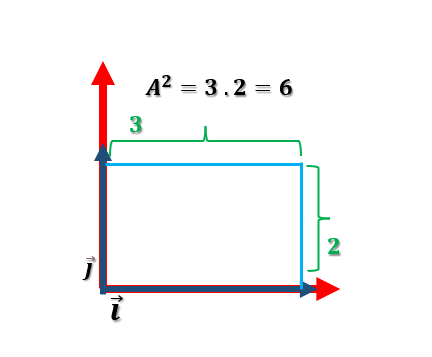
Si nos fijamos detenidamente, podemos ver que el área ha incrementado de 1 a 6. Precisamente esto es lo que nos mide el determinante de una matriz; nos está diciendo la distorsión que ha sufrido el vector en el proceso de transformación lineal.
¿Quieres seguir aprendiendo?
Ahora que has visto cómo funciona el determinante de una matriz, puedes dar un paso más para acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral. No te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra y de alta intensidad en la que adquirirás, en pocos meses, todos los conocimientos teóricos y prácticos que te ayudarán a obtener tu trabajo deseado. ¡Entra ya para solicitar información y anímate a cambiar tu futuro con la guía de los mejores profesionales!



