El Kernel PCA (Principal Component Analysis o análisis de componentes principales) es una reformulación del algoritmo PCA utilizando un kernel, lo que permite aplicar PCA en un espacio de alta dimensionalidad. En vez de calcular los autovectores de la matriz de covarianza, estos se calculan a partir de la matriz de kernel PCA. Así, las distancias se miden en el espacio de características de alta dimensionalidad.
Algunas generalidades del kernel PCA
El PCA es un método exclusivamente lineal, es decir, solo se puede aplicar a conjuntos de datos que son linealmente separables.
Lo que hace el kernel PCA es utlizar una función de kernel para proyectar un conjunto de datos en un espacio de características de mayor dimensión, donde puede ser linealmente separable.
En cierto sentido, el kernel PCA aplica la misma lógica que los SVM o support vector machines.
Existen diferentes tipos de kernel PCA, entre ellos el kernel lineal, el kernel polinomial y el kernel gaussiano.
Ejemplo de Kernel PCA
Veamos cómo funciona el Kernel PCA por medio de un ejemplo. Vamos a usar un dataset denominado make moons y vamos a ver lo que pasa. Por supuesto, lo primero que haremos será importar el dataset que utilizaremos desde scikit learn; también importaremos la librería necesaria para trabajar con el kernel PCA.
#Ejemplo de Kernel PCA
from sklearn.datasets import make_moons
from sklearn.decomposition import KernelPCA
X, y = make_moons (n_samples = 100, random_state = 123)
XKPCA = KernelPCA (n_components = 2, kernel = 'rbf', gamma = 15). fit_transform (X)
plt.figure (figsize = (16, 6))
# figure 1
plt.subplot (1, 2, 1)
plt.scatter (x [y == 0, 0], x [y == 0, 1], color = 'red', alpha = 0.5)
plt.scatter (x [y == 1, 0], x [y == 1, 1], color = 'blue', alpha = 0.5)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)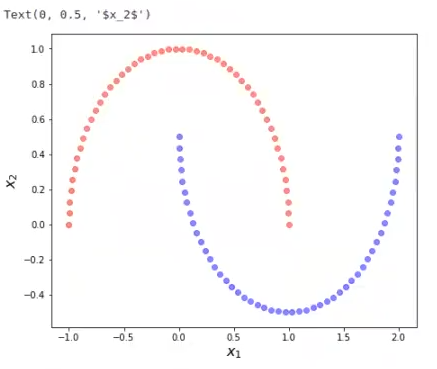
Esto es make moons, el dataset que tenemos. Como podemos observar, no es linealmente separable. Si aplicamos un kernel al make moons, lo que va a hacer este kernel es llevar el conjunto de datos a otro espacio de dimensionalidad. Veamos cuál es:
#Ejemplo de Kernel PCA
plt.figure (figsize = (16, 6))
# figure 2
plt.subplot (1, 2, 2)
plt.scatter (XKPCA [y == 0, 0], XKPCA [y == 0, 1], color = 'red', alpha = 0.5)
plt.scatter (XKPCA [y == 1, 0], XKPCA [y == 1, 1], color = 'blue', alpha = 0.5)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
plt.show ()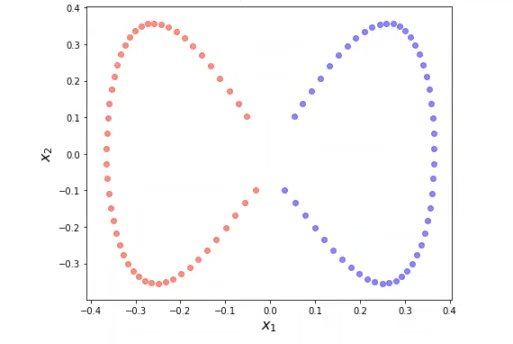
Al aplicar esa transformada, este se convierte en un problema linealmente separable.
Veamos otro ejemplo. Vamos a hacer lo mismo que hemos hecho en el dataset make moons, pero ahora lo haremos con otro conjunto de datos, denominado make circles.
Vamos a aplicar kernel PCA sobre el siguiente ejemplo y vamos a representar el resultado:
#Ejemplo de Kernel PCA
from sklearn.datasets import make_circles
X, y = make_circles (n_samples = 1000, random_state = 123, noise =0.1, factor = 0.2)
XKPCA = KernelPCA (n_components = 2, kernel = 'rbf', gamma = 15).fit_transform (X)
#Ejemplo de Kernel PCA
plt.figure (figsize = (16, 6))
plt.subplot (1, 2, 1)
plt.scatter (X [y == 0, 0], X [y == 0, 1], color = 'red', alpha = 0.5) plt.scatter (x [y == 1, 0], X [y == 1, 1], color = 'blue', alpha = 0.5)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
plt.show ()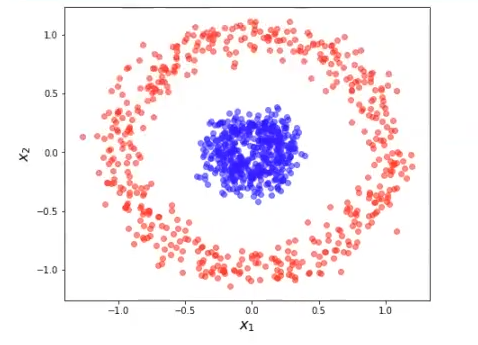
Este es el dataset original de make circles. Después de aplicar la transformación kernel, lo que tenemos es el siguiente resultado:
#Ejemplo de Kernel PCA
plt.figure (figsize = (16, 6))
plt.subplot (1, 2, 2)
plt.scatter (XKPCA [y == 0, 0], XKPCA [y == 0, 1], color = 'red', alpha = 0.5)
plt.scatter (XKPCA [y ==1, 0], XKPCA [y == 1, 1], color = 'blue', alpha = 0.5)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("Sx_2$", fontsize = 16)
plt.show ()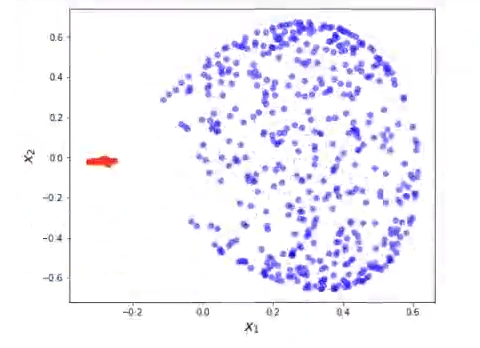
Vamos a variar los parámetros del kernel PCA:
#Ejemplo de Kernel PCA
XKPCA = KernelPCA (n_components = 2, kernel = 'rbf', gamma = 1.5).fit_transform (X)Si hacemos esto, lo que conseguimos es variar la transformación:
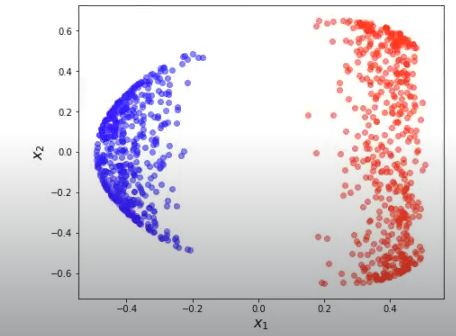
En este caso le modificamos el valor gamma, que inicialmente era de 15 y en este último resultado lo hemos puesto en 1.5 para que se vea más claramente la diferencia y la clasificación linealmente separable entre las dos instancias del conjunto de datos de make circles.
¿Quieres seguir aprendiendo sobre Big Data?
Para que cumplas tus sueños y sigas aprendiendo sobre el mundo tecnológico, que ofrece excelentes y numerosas oportunidades en el mercado laboral, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación intensiva adquirirás todos los conocimientos teóricos y prácticos para que sigas tu camino hacia el éxito en pocos meses. ¡No esperes más para obtener lo que quieres y solicita información ahora!











