¿Sabes qué es el learning rate en el descenso de gradiente y cómo aplicarlo en tus procesos de machine learning? Cuando estamos realizando optimización con descenso de gradientes, lo que queremos es encontrar el valor de w que hace mínima la función f (x), es decir, vamos a encontrar el arg min f (x).
Para ello se deben seguir algunos pasos y existe una fórmula a usar:
x := x – η . ∇ f (x)
En esta fórmula, el parámetro ∇ corresponde al learning rate en el descenso de gradiente. Este parámetro es el encargado de medir el tamaño de cada iteración en el proceso del descenso de gradientes, es decir, cuánto nos vamos a mover en cada paso.
El learning rate en el descenso de gradiente
Veamos con un ejemplo cómo funciona el learning rate en el descenso de gradiente. Tenemos este ejemplo:
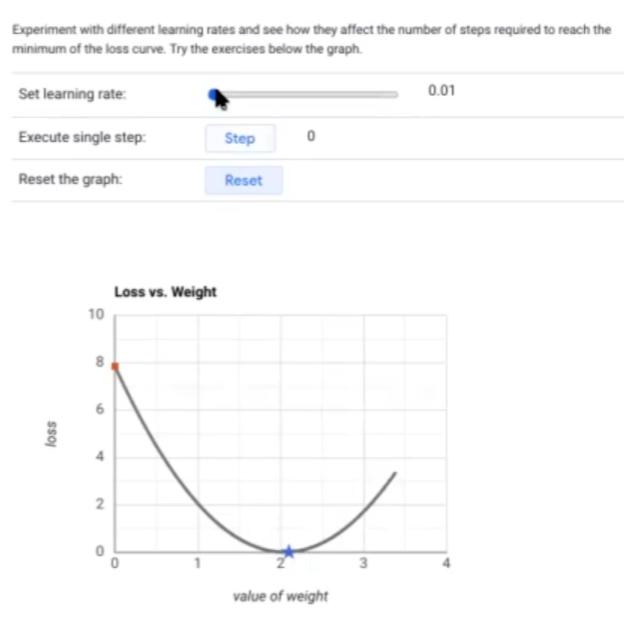
Lo que queremos es llegar a la estrella azul. Si el learning rate es 0.01, vamos a ir ejecutando los pasos o steps (1, 2, 3, 4, 5, … n) y vemos cómo, poco a poco, el punto rojo se va acercando a la estrella. Como podemos observar, se tarda muchísimo en llegar:
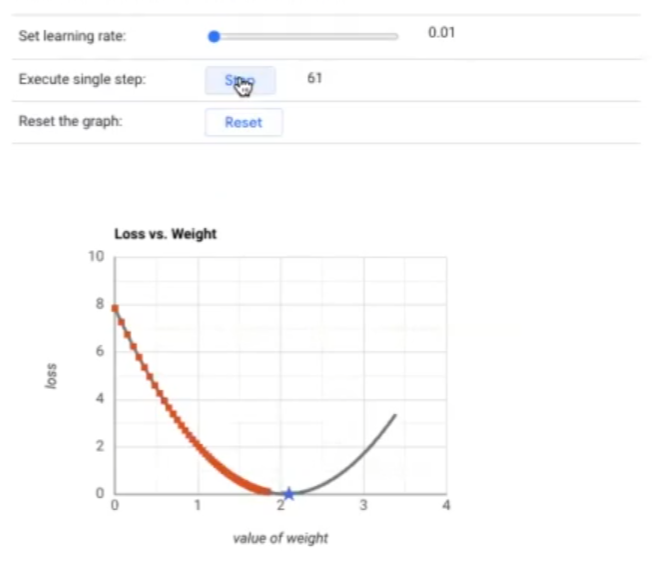
En cambio, si incrementáramos el rate un poquito, por ejemplo, un 0.03, vemos que los pasos que se dan son más grandes y que se tarda menos en llegar al objetivo:
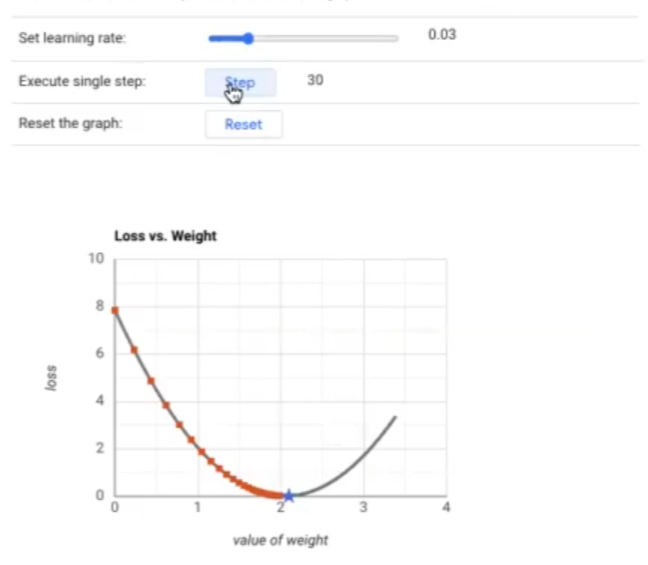
Es por esa razón que decimos que el learning rate en el descenso de gradiente hace este método de optimización iterativo.
El learning rate en el descenso de gradiente (con Python)
Veamos un ejemplo en Python sobre el learning rate en el descenso de gradiente.
Primero importamos las librerías necesarias, que en este caso son Numpy y Matplotlib:
#Este código emula más o menos lo que hemos visto en el ejemplo anterior
#learning rate en el descenso de gradiente
import numpy as np
import matplotlib.pyplot as plt
class GD ():
def__init__ (self, eta = 0.1, x0 = 0, max_iter = 50, diff_to_stop = 0.01)
self.x0 = x0 #Randomly initialize any value
self.delta = delta #Used for gradient calculations
self.eta = eta #Learning rate
self.diff_to_stop = diff_to_stop #stop the algorithms
self.max_iter = max_iter #When to stop
def run (self, f, plot_method = None)
plt.figure (figsize = (8, 4))
xx = np.linspace (-10, 10, 100)
yy = f (xx)
plt.plot (xx, yy)
plt.grid ()
x_new = self.x0
iter_no = 0
while True:
iter_no += 1
#learning rate en el descenso de gradiente
#Main algorith
x = x_new #note: x_new is the position of the previos move
grad = (f (x + self.delta)- f (x) / self.delta
x_new = X - self.eta * grad
#End of main algorithm
if plot_method is 'scatter':
plt.scatter (x_new, f (x_new), color = 'r')
else:
plt.arrow (x, f (x), x_new - x, f (x_new) - f (x), head_width = 0.3)
step_size = np.abs (x_new - x)
if step_size <= self.diff_to_stop:
print ('Sucessfully converged with a setp size of {} after finish')
break
elif iter_no == self.max_iter:
print ('Max iterations completed: Convergence cannot be guarantied')
plt.scatter (x_new, f (x_new), s = 200, marker = ' * ')
break
elif iter_no == self.max_iter:
print ("Mark iterations completed: Convergence cannot be guarantied")
plt.scatter (x_new, f (x_new), s = 200, marker = ' * ')
break

Vamos a analizar qué sucede cuando modificamos los parámetros:
- Incrementa el número de iteraciones a 50. (Increase the maximum number of iterations to 50).
- Cambia el learning rate a diferentes valores de η ∈ {0.05, 0.1, 0.8, 1.1}
#learning rate en el descenso de gradiente
def f (x, p = 1, q = 0, r = 0):
return p * (x - q) ** 2 + r
GD (eta = 0.00002, x0 = 8, max_iter = 5, diff_to_stop = 0.01, delta = 0.01).run (f)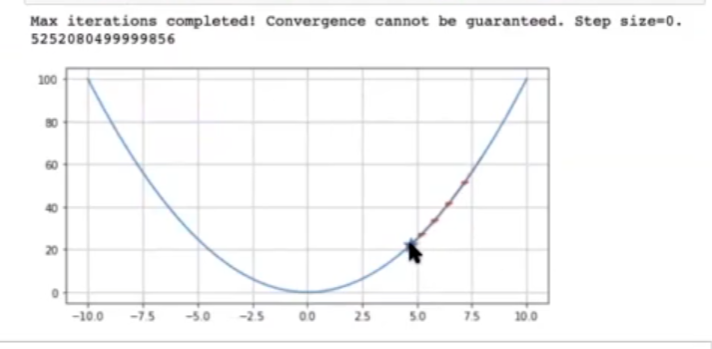
Comenzando en el punto 8 y haciendo 5 iteraciones no alcanzaríamos a llegar al mínimo.
Si cambiáramos el learning rate, de 0.00002 a 0.01, daría pasos más grandes y se iría acercando más al mínimo.
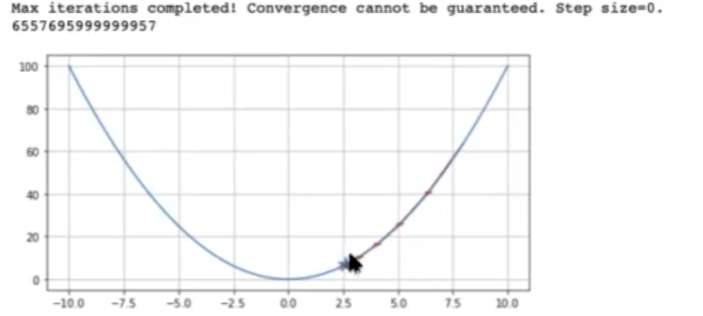
¿Qué sucede en este caso?
f (x) = -exp (- (x – 2)2) – 0.5 exp (- (x + 2)2)
Sugerencia: max_iter en 100, x0 en -3.
Veamos otro caso:
#learning rate en el descenso de gradiente
def f_multimodal (x):
return -np.exp (- (x - 2) ** 2) - 0.5 * np.exp (- (x + 2) ** 2)
GD (eta = 0.1, x0 = -3, max_iter = 100, diff_to_stop = 0.01, delta = 0.01).run
#Local minimum —¿Alguna solución?—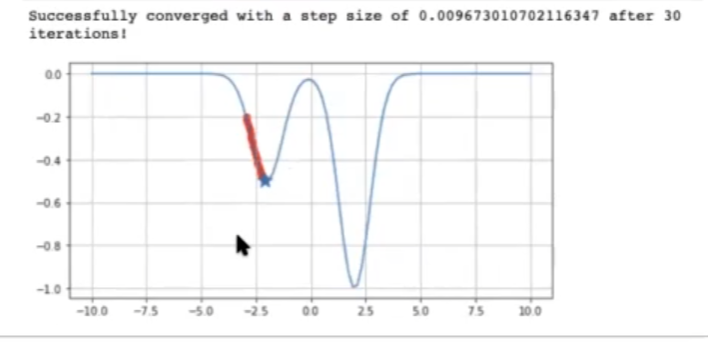
¿Quieres aprender más?
El Big Data es una de las áreas con más demanda laboral hoy en día, además de tener las mejores medias salariales. Para poder acceder a este tipo de opciones de empleo, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que aprenderás a nivel teórico y práctico. Con la guía de profesionales en el sector y el apoyo de nuestra Bolsa de Talento, podrás obtener el trabajo de tus sueños en pocos meses. ¡No esperes más para impulsar tu futuro y solicita más información ahora!



