¿Qué es el menor complementario?

Si estás inmerso en el mundo del Big Data y el machine learning, seguro que te has topado alguna vez con los términos menor complementario y adjunto de un elemento. Por ello, en este artículo, te enseñaremos qué es el menor complementario y cuál es la relación que este concepto guarda con el adjunto de una matriz.

Adjunto de un elemento

Se llama A_ij de un elemento a_ij al valor:

A_ij = (-1)^{i + j}. a_ij

Es decir, si i + j es par, coincide el adjunto con el menor complementario, mientras que si i + j es impar, tendrán valores opuestos.

¿Cómo lo hace Numpy? — Menor complementario

Dada una matriz cuadrada de orden n, A = (a_ij), se denomina menor complementario a_ij de un elemento a_ij al determinante de la matriz de orden n – 1, que resulta de suprimir en la matriz A la fila i y la columna j.

Observa esta matriz:

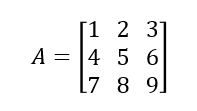
El menor complementario al elemento a₁₁ = viene dado por:

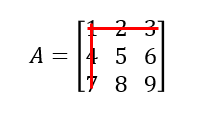
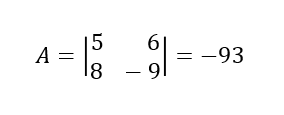
El menor complementario al elemento a₂₂ = 5 viene dado por:

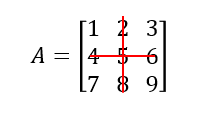
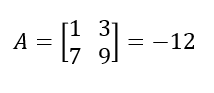
Numpy internamente no aplica la regla de Sarrus, porque a nivel computacional no es tan eficiente como calcular el determinante aplicando el menor complementario. Además, no es extensible a matrices de mayor orden.

def getMatrixMinor (m, j):
       return [row [:j] + row [j + 1:] for row in (m [:0] + m [1:])]

defgetMatrixDeterminant (m):
     if  len (m) == 2:
          return m [0] [0] * m [1] [1] - m [0] [1] * m [1] [0]

     determinant = 0
for c in range (len (m)):
      minor_matrix = getMatrixMinor (m, c)
      determinant += ((-1) ** c) * m [0] [c] * getMatrixDeterminant (minor_matrix)
      return determinant      

D = [[5,   0,   2],   [3,   1,   1],   [0,   1,   2]]
getMatrixDeterminant (D)

11

%timeit getMAtrixDeterminant (D)

4.14 µs

%timeit np.linalg.det (D)

6389 µs

¿Quieres seguir aprendiendo?

Ahora que has visto cómo funciona el menor complementario, qué es y cómo se relaciona con el adjunto de un elemento o de una matriz, puedes seguir adelante. Para destacar en una de las disciplinas más demandadas y mejor pagadas del mundo laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación íntegra y de alta intensidad, adquirirás, en pocos meses, los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!