El producto escalar o producto interno es el resultante de la multiplicación de dos vectores.
En este artículo, veremos un poco más a fondo en qué consiste este producto.
Producto escalar
Vamos a empezar definiendo el vector u, que tiene n componentes. Luego, tenemos el vector v, que tiene, al igual que el vector u, n componentes. El producto escalar no es más que multiplicar los componentes. El resultado que nos va a dar es un número, es decir, el producto interno o escalar es, a su vez, un escalar.
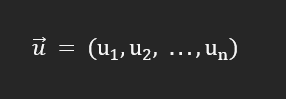
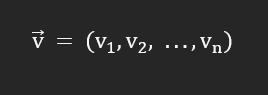
Vamos a dibujar dos vectores, el u y el v. La ecuación que rige el producto interno o escalar es:
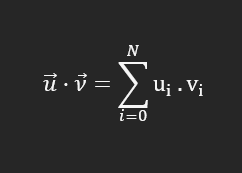
Esto significa que el producto escalar es igual al sumatorio de la multiplicación de cada componente de un vector con los componentes de otro vector.
Esta ecuación la podemos desarrollar de otra forma. Cogemos el primer componente del vector u y el primer componente del vector v y los multiplicamos. Ahora, le sumamos la multiplicación de los segundos componentes, la multiplicación de los terceros componentes, y así sucesivamente con todos los componentes que tengamos.
El sumatorio es lo que nos está definiendo esta suma:
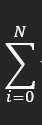
Esto lo realizamos N veces, donde N corresponde al número de componentes.
Ejemplo de producto escalar
Veamos un ejemplo de este producto escalar para entenderlo mejor. Tenemos, por tanto, un vector u con valores [2 3 1] y un vector v con valores [1 4 5]. Vamos a hacer el producto escalar de estos dos vectores:
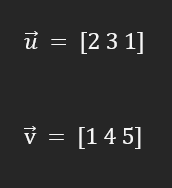
Si adaptamos la fórmula del producto escalar a nuestro ejemplo, sería:
2 . 1 + 3 . 4 + 1. 5 = 2 + 12 + 5 = 19
Ya vemos cómo el resultado del producto escalar es otro escalar.
Utilidad del producto interno o escalar
Este producto es de muchísima utilidad internamente. Veamos dónde radica su importancia.
Tenemos el vector u y luego el vector v. El producto interno o escalar no es más que la proyección del vector u sobre el vector v. Los vectores, por supuesto, tienen un ángulo entre ellos.
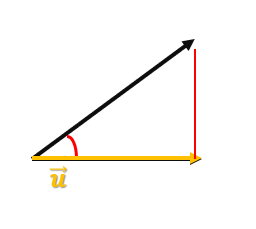
En vez de tener la proyección de u (representada por la flecha amarilla) colapsada en el mismo punto, vamos a intentar moverla. De este modo, tendríamos v, y si movemos la proyección y ponemos el origen de la misma justo donde acaba el vector v, este resultado sería, con el ejemplo del caso anterior, igual a 19. Veamos:
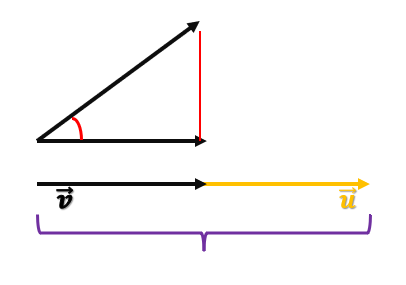
¿Qué sigue?
Para que cumplas tus sueños y sigas aprendiendo sobre el mundo tecnológico, en el que encontrarás excelentes oportunidades para desarrolladores y aspirantes a data scientist, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación íntegra e intensiva adquirirás todos los conocimientos teóricos y prácticos para lograr tus objetivos. ¡No esperes más triunfar en el mundo IT y solicita información ahora!











