El producto vectorial de dos vectores u y v, a diferencia del producto interno o producto escalar, el cual produce un escalar, tiene como resultado un vector. Una de las características de dicho vector es que resulta ser perpendicular al plano generado por los vectores u y v. Si ambos vectores son no nulos, la única forma de que el vector resultante sea nulo es que tanto u como v no formen un plano y que, por lo tanto, sean colineales.
¿Cómo calcular el producto vectorial?
La biblioteca numpy cuenta con una función que permite obtener el producto vectorial de manera sencilla. La función cross(u, v) devuelve un array con el producto vectorial.
Además, el módulo del producto vectorial es igual al área del paralelogramo del lado asociado a ambos vectores.
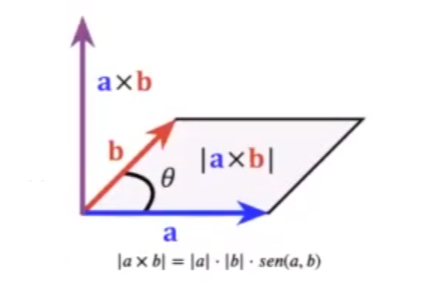
En este artículo veremos cómo se calcula el producto vectorial usando numpy. Más adelante veremos en profundidad cómo numpy lo calcula internamente, ya que hace falta tener conocimientos de determinantes que veremos en detalle más adelante.
Vamos a hacer una prueba definiendo los vectores u y v, dos vectores bastante simples:
u = np.array ([3, -2, 4])
v = np.array ([1, 2, -3])
print (u, v)[3 -2 4] [1 2 -3]
El producto vectorial viene definido por .cross, que es la función que tiene numpy implementada para este tipo de productos:
c = np.cross (u, v)
print (c)[-2, 13 8]
Como vemos aquí, el resultado es otro vector perpendicular a u y v. Además, el módulo del vector C es el área del paralelogramo del lado asociado a ambos vectores.
El módulo del vector resultante es el área señalada en verde:
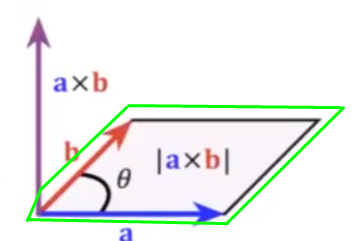
Vamos a calcular esta área usando .norm:
np.linalg.norm (c)15.394804318340652
Como hemos mencionado antes, el producto vectorial de dos vectores colineales es nulo:
u = np.array ([1, -9, 14])
v = np.array ([-4, 36, -56])
C = np.cross (u, v)
print (C)[0 0 0]
En otras palabras, si el plano señalado en verde no existe, el resultado del vector morado es nulo.
El resultado es 0, ya que el segundo vector se obtiene del primero multiplicándolo por -4 y, por tanto, ambos vectores son colineales.
Ahora que hemos visto cómo funciona el producto vectorial, podemos seguir aprendiendo sobre Big Data, una de las disciplinas con mayor demanda de la actualidad y mejor pagadas. El Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp es una formación intensiva e íntegra en la que podrás aprender a nivel teórico y práctico todo lo necesario para entrar en el mercado laboral de manera rápida y eficiente. ¡Anímate a continuar cambiando tu futuro y entra ahora para pedir más información!











