El Teorema de Bayes en estadística Big Data es uno de los cálculos de probabilidad aplicados a un evento en la población de los datos procesados. En suma, es uno de los más utilizados, ya que su fórmula es relativamente simple y su funcionamiento muy efectivo en el análisis estadístico.
De hecho, contar con este saber dentro de los conocimientos base para llevar a cabo algún estudio de datos de este tipo es de suma importancia para un buen data scientist en el manejo de los macrodatos por medio de la estadística. Por ello, en este post, te explicamos qué es y cómo funciona el teorema de Bayes en estadística Big Data.
Teorema de Bayes en estadística Big Data
El teorema de Bayes en estadística Big Data describe la probabilidad de un evento basado en conocimientos previos que pueden estar relacionado con dicho evento.
Por otra parte, su fórmula para la inscripción es bastante simple:
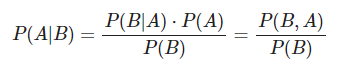
Por medio de esta, se expone el comportamiento de las variables estudiadas, donde A y B son las variables aleatorias y P(B)≠0:
- P(A|B) es la probabilidad condicional del evento A, sabiendo que ha ocurrido B.
- P(B|A) es la probabilidad condicional del evento B, sabiendo que ha ocurrido A.
- P(A) y P(B) es la probabilidad de observar A y B de forma independiente. S conoce como la probabilidad marginal.
- P(B,A) o P(B ∩ A): es la probabilidad de que ambos eventos, A y B, ocurran a la vez.
- Si son sucesos independientes: P(B,A)=P(B)·P(A).
- Si son sucesos dependientes: P(B,A)=P(B|A)·P(A).
Ahora, para ejemplificar cómo funciona el teorema de Bayes en estadística Big Data, imagina que puedes ver dentro de x cuadrado verde unos disparos rojos y blancos sobre un barco. En total, hay 35 disparos: 20 rojos y 15 blancos.
La probabilidad de elegir un disparo rojo al azar es:
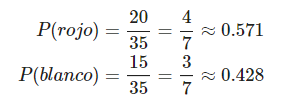
La probabilidad de, en ese cuadrado, acertar al barco es:
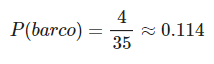
Si sabes que se ha realizado un disparo blanco, ¿cuál es la probabilidad de que haya dado en el barco?
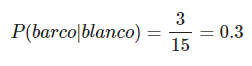
Si sabes que se ha realizado un disparo rojo, ¿cuál es la probabilidad de que le haya dado al barco?
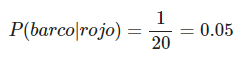
Aplica el teorema de Bayes
El barco ha sido alcanzado por un disparo. ¿Cuál es la probabilidad de que ese disparo sea rojo?
Si te están preguntando por P(rojo|barco) y ya conoces P(barco|rojo), P(barco) y P(rojo), entonces por el teorema de Bayes en estadística Big Data sería:
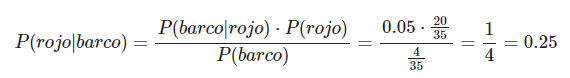
El barco ha sido alcanzado por un disparo. ¿Cuál es la probabilidad de que ese disparo sea blanco?
Te están preguntando por P(blanco|barco), de manera que conoces a P(barco|blanco), P(barco) y P(blanco), así que por el teorema de Bayes en estadística Big Data sería:
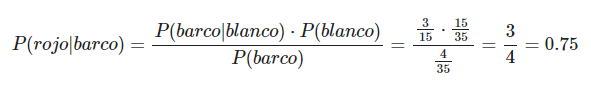
Probabilidad conjunta
¿Cuál es la probabilidad de que un disparo de en el barco y, además, sea rojo?
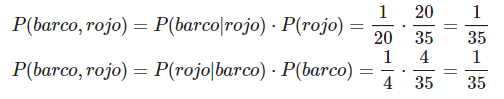
Sigue aprendiendo del Big Data
Por medio de este post, te has podido familiarizar con lo que es y cómo funciona el teorema de Bayes en estadística Big Data, de manera que ahora podrás implementarlo en tu estudio de los macrodatos cuando resulte necesario hacer uso de este. No obstante, debes tener en cuenta que un buen data scientist debe contar con muchos más conocimientos sobre este campo, ¡así que te animamos a seguir aprendiendo sobre el manejo del Big Data!
Para continuar formándote sobre el Big Data y sus herramientas, desde KeepCoding te recomendamos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. A través de esta formación intensiva, aprenderás a dominar los conocimientos necesarios para implantar cualquier tipo de arquitectura, de manera que, en menos de nueve meses, serás todo un experto en el manejo de los macrodatos. ¡No lo dudes más e inscríbete ya para convertirte en un experto del sector IT!











