¿Qué es el Hierarchical DBSCAN (HDBSCAN)?

En este artículo te explicaremos qué es el Hierarchical DBSCAN y cómo usarlo por medio de un ejercicio de aplicación.

El Hierarchical DBSCAN esencialmente calcula la jerarquía de todos los clústeres de DBSCAN para un minPts dato. Luego utiliza una estabilidad basada en el método de extracción para encontrar cortes óptimos en la jerarquía, por lo que produce una solución plana.

Ejercicio aplicando Hierarchical DBSCAN

Hay que tener en cuenta que minPts no solo actúa como un tamaño mínimo de clúster para detectar, sino también como un factor de suavizado de las estimaciones de densidad calculado implícitamente desde Hierarchical DBSCAN.

set.seed (123)
N <- 1000
x <- c (rnorm (N, mean = 1, sd = 0.5), rnorm(N, mean = 3.5, sd = 0.5), rnorm (2 * N, mean = 8, sd = 1))
df <- data.frame (x = x, y = runif (length (x)))
head (df)

	x	y
	<dbl>	<dbl>
1	0.7197622	0.5779101
2	0.8849113	0.4888454
3	1.7793542	0.7421904
4	1.0352542	0.2256090
5	1.0646439	0.7488911
6	1.8575325	0.85248685

library (ggplot2)
options (repr.plot.height = 2, repr.plot.width = 6, repr.plot.res = 300)

ggplot (df, aes (x = x, y = y)) + geom_point (size = 0.1) + geom_density2d (h = c (1, 2))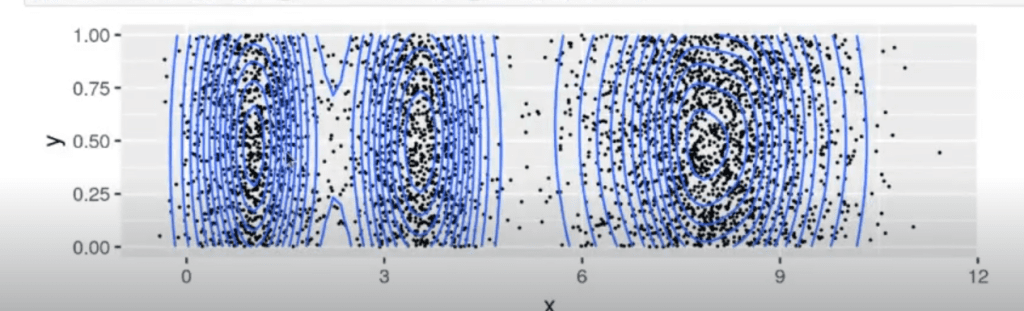

ggplot (df, aes (x = x)) + geom_density (bw = 0.15)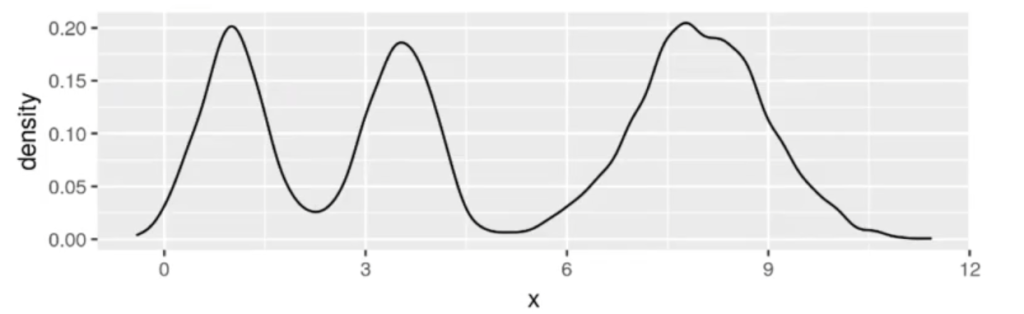

library (dbscan)
minPts <- 500

cl <- hdbscan (df [ , c ("x", "y")], minPts = minPts.gen_simplified_tree = TRUE, gen_hdbscan_tree = TRUE)

Hierarchical DBSCAN no es más que una ejecución de DBSCAN para diferentes valores de epsilon.

Vamos a demostrarlo a continuación:

options (repr.plot.height = 4, repr.plot.width = 6, repr.plot.res = 300)

plot (clshc)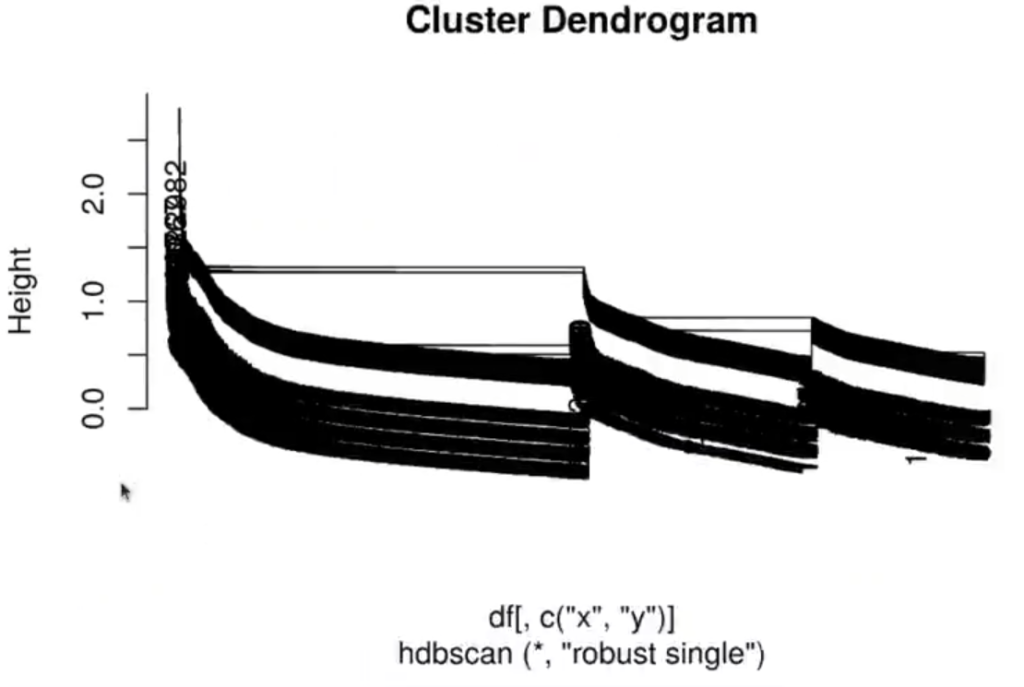

## cutree no distingue el ruido como 0, por lo que creamos un nuevo método para hacerlo manualmente
cut tree <- function (hcl, eps, core_dist) {
cuts [which (core_dist > eps)] <- 0 #Usa la distancia del núcleo para distinguir las opciones de corte de ruido
cuts
}
cor_dist <- kNNdist (df [ , c ("x", "y")], k = cl$minPts - 1)
plot (sort (core_dist), t = 'l')
options (repr.plot.height = 2, repr.plot.width = 6, repr.plot.res = 300)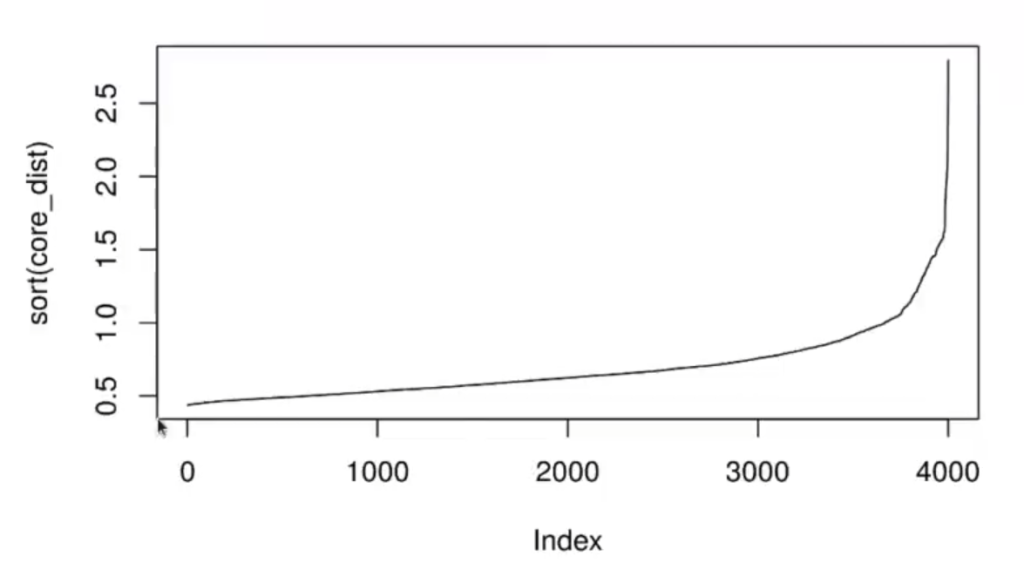

eps_value = 0.7
#eps_value = 1.2
#eps_value = 1.5

cut cl <- cut_tree (cl$hc, eps_value, core_dist)

dbscan_cl <- dbscan (df [ , c ("x", "y")], eps = eps_value, minPts = minPts, borderPoints = F)

(all.equal (rle (cut_cl) $lengths, rle (dbscan_clscluster) slengths) == "TRUE")
#Ejemplo de como funciona rle
#c (rep (6 : 10, 1 : 5), 6, 6)
#rle (c (rep (6 : 10, 1 : 5), 6, 6))

TRUE

cut cl <- cutree (cl$hc, h = 1.2)
table (cut_cl)
table (dbscan_cl$cluster)

cut_cl
0 1319	1 671	333 627	705 1383
0 1319	1 671	2 627	3 1383

dfscluster <- factor (cut_cl)
#df$cluster <- factor (dbscan_cl$cluster)
ggplot (df, aes (x = x, y = y, color = cluster)) + geom_point (size = 0.1)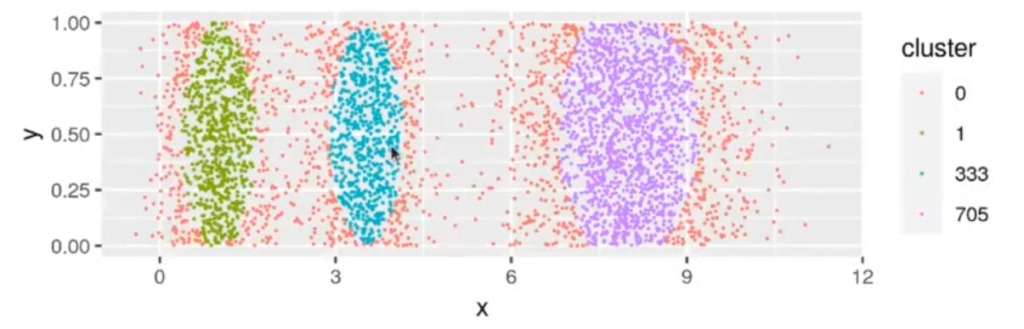

Estabilidad de clústers

cl <- hdbscan (df [ , c ("x", "y")], minPts = minPts.gen_simplified_tree = TRUE, gen_hdbscan_tree = TRUE)
cl

HDBSCAN (HIERARCHICAL dbscan) clustering for 4000 objects.

Parameters: minPits = 500

El clustering contiene 3 clúster(s) y 411 puntos de ruido.

0	1	2	3
411	1876	855	858

Avalaible fields: cluster, minPts, cluster_scores, membership_prob, outlier_scores, hc, hdbscan_tree, simplified_tree

df$cluster <- as.factor(cl$cluster)
options (repr.plot.height = 2, repr.plot.width = 6, repr.plot.res = 300)
ggplot (df, aes (x = x, y = y, color = cluster)) + geom_point (size = 0.1)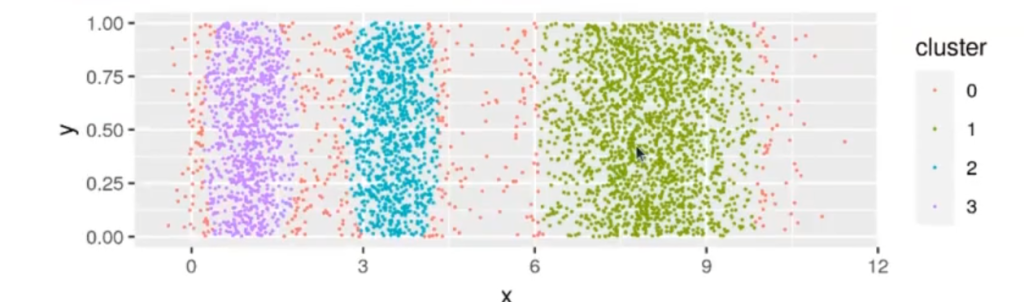

Continuando con el ejercicio de Hierarchical DBSCAN, para calcular la estabilidad definimos λ = l / i. Suponiendo que vamos probando con valores E decrecientes, lo que equivale a λ creciente. Para un clúster podemos definir los valores λ_birth y λ_death como el valor de λ en el cual el clúster aparece (como división de un clúster mayor) y desaparece al dividirse en clústeres más pequeños.

Podemos definir λ como el valor en el intervalo [λ_birth , λ_death], en el que el punto p se escapa del clúster estudiado.

Se define la estabilidad de un clúster como:

Finalmente, se hace un recorrido de abajo arriba del árbol; empezando por las hojas, calculamos la estabilidad de cada uno de los clústeres que van saliendo a medida que subimos (disminuimos).

¿Qué sigue?

El Hierarchical DBSCAN es un algoritmo de mucha utilidad en algunas ocasiones en las que necesitas hacer procesos de clustering. Recuerda que, si quieres seguir aprendiendo sobre todas estas temáticas, puedes inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva con la que en muy pocos meses podrás adquirir todos los conocimientos necesarios para incursionar en el mercado laboral. ¡Anímate y solicita más información!