¿Sabes qué es la dimensionalidad de vectores y por qué es tan importante en el machine learning? Recordemos que los vectores de software tienen una gran cantidad de números que vienen denotados por esa cantidad y están representados por la letra N. La N indica la dimensión del vector, es decir, su número de componentes.
Problema de la dimensionalidad de vectores en machine learning
¿Qué sucede con la dimensionalidad de vectores en machine learning? Hay algunos modelos que tienen problemas para trabajar con esta gran cantidad de datos, es decir, hay modelos que no funcionan muy bien cuando las secuencias son muy largas, cuando la dimensión del vector es muy grande.
¿Qué pasa, entonces, cuando tenemos una dimensionalidad de vectores muy grande? Tenemos que hacer un proceso que se denomina dimensionality reduction.
Dimensionality reduction
La dimensionality reduction y todas las técnicas abarcadas en esta nos permiten reducir la dimensionalidad de vectores. Esto nos ayuda con los modelos que tienen problemas para tratar con el número de componentes.
Métodos para reducir la dimensionalidad de vectores
Una de las técnicas que sirve para reducir la dimensionalidad de vectores es el PCA, cuya sigla quiere decir principal components analysis y se traduce como análisis de componentes principales. Este método busca reducir la dimensionalidad de nuestro vector, pero intentando conservar la mayor cantidad de información disponible en el vector.
Imaginemos que tenemos el vector [1,2, 20, 30, 70, 25…]. Este vector tiene 2000 componentes, pero, ¿cómo denotamos esto matemáticamente? Lo que decimos es que pertenece a un espacio vectorial R elevado a N (RN). La R es porque viene de los números reales y los componentes pueden tener cualquier valor, ya sea positivo o negativo, con decimales o sin decimales. Lo que la N está indicando es, al igual que con nuestros vectores habitualmente, el número de componentes del vector. Es decir, la notación matemática de los componentes de este vector en específico quedaría R2000.
Entonces, lo que nos permite usar un método para reducir la dimensionalidad de vectores, como es el principal components analysis, es la siguiente gráfica:
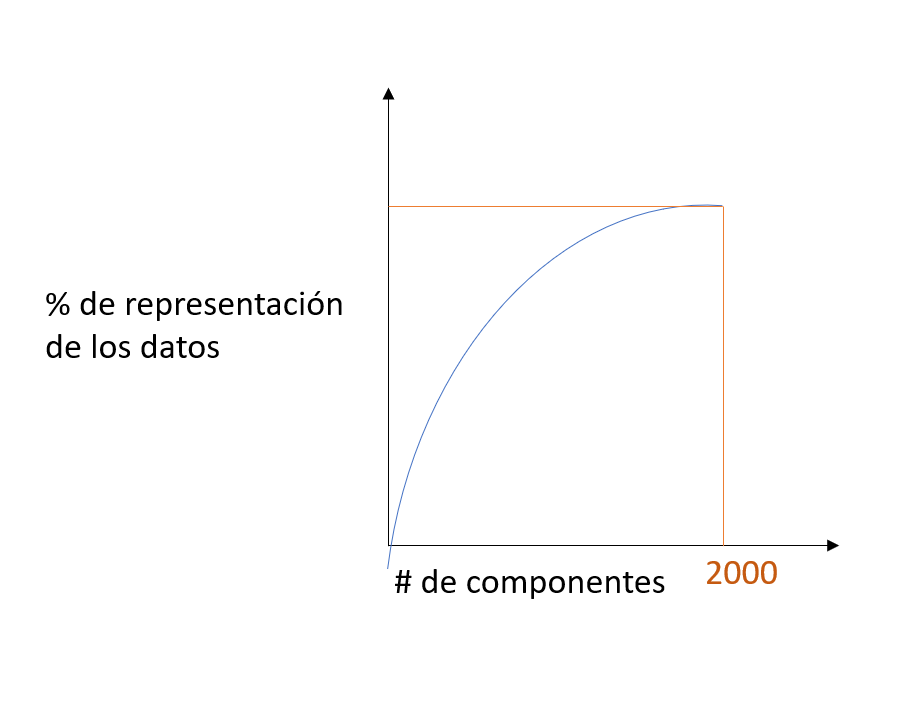
El eje x de la gráfica corresponde al número de componentes. El eje y corresponde al porcentaje de representación de los datos. El límite de y es el 100%. ¿Qué quiere decir esta gráfica? Pues esta surge cuando hacemos, por ejemplo, un principal component analysis.
Lo que nos está representando la gráfica es el dibujo del número de componentes con respecto al porcentaje de representación de los datos originales. Esto hace referencia a, conforme reducimos el número de componentes de nuestro vector, qué porcentaje de representación de los datos originales tiene el vector resultante.
Explicado de otro modo, podríamos decir que tenemos un vector de 2000 componentes y usamos PCA para reducir ese vector a 100 componentes. Si lo pensamos detenidamente, reducir una cantidad tan grande a una tan pequeña y sin perder información debe tener algún truco.
Por supuesto que perdemos información, y esa información viene representada por la gráfica que tenemos más arriba. Esto es, precisamente, lo que significa el porcentaje de representación de los datos.
Es decir, si tenemos 100 componentes, según la gráfica, habríamos perdido muchísima información, no datos, pero sí información. Esta podría o no resultarnos relevantes para nuestros análisis futuros.
Entonces, si en vez de reducir tanto, reducimos, por ejemplo, solo hasta 1000, no perderemos tanto y habremos reducido la dimensionalidad de vectores a la mitad.
Si hacemos una dimensionality reduction juiciosa, será mucho más fácil trabajar con nuestros vectores sin perder cantidades de información astronómicas.
¿Quieres seguir aprendiendo más sobre Big Data?
Para que cumplas tus sueños y sigas aprendiendo sobre el mundo tecnológico, que ofrece excelentes oportunidades, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación intensiva adquirirás todos los conocimientos teóricos y prácticos para que sigas tu camino hacia el éxito. Contarás, además, con los mejores profesionales para acompañarte en tu proceso formativo y apoyarte en todo lo que necesites. ¡No esperes más para obtener lo que quieres y solicita más información ahora!











