La distancia de Cook nos sirve para detectar outliers, valores cuyo valor influye mucho en la salida de la regresión lineal. En este post, profundizamos en qué es la distancia de Cook y cómo calcularla.
Calcular la distancia de Cook
Para entender qué es la distancia de Cook, es imprescindible saber cómo calcularla. Se calcula mirando la diferencia entre el modelo completo con todas las muestras menos el modelo generado eliminando la muestra bajo estudio. La distancia de Cook para la muestra / se puede calcular como:
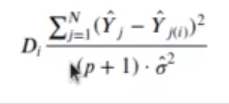
// distancia de Cook
In [72]: plot (cooks.distance (mode_powerplant))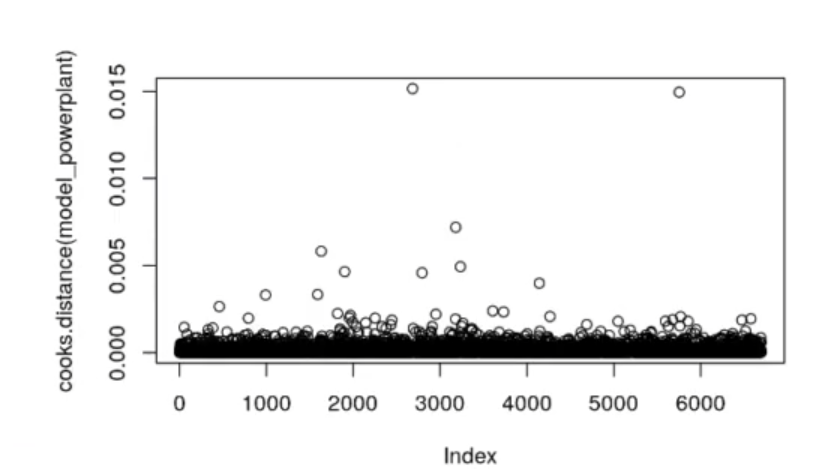
Combinación de modelos con grupos de test
La distancia de Cook hace eso, pero sacando una variable de la ecuación. Es decir, el dataset de train crea un nuevo modelo sin un punto y ve si ha cambiado mucho o no; luego, pasa a otro y verifica lo mismo, y así sucesivamente.
Si el hecho de insertar o sacar el punto cambia mucho la regresión, tiene una gran importancia, ya que modifica muchísimo la gráfica y se genera una especie de outlier.
Podemos eliminar ese outlier del siguiente modo:
// distancia de Cook
In [73]: powerplant.train_clean <- powerplant.train [cooks.distance (model_powerplant) <0.005,]
model_powerplant_clean<-lm(PE-AT+V+AP+RH,data = powerplant.train_clean)
summary(model_powerplant_clean)Call:
Im(formula = PE – AT + V + AP + RH, data = powerplant, train_clean)
Residuals:
Min: -26.9815
1Q: -3.1315
Median: -0.1563
3Q: 3.1611
Max: 17.7887
Coefficients:
| Estimate | Std. | Error | t value | Pr(>ltl) | ||
| (Intercept) | 464.045977 | 11. | 278761 | 41.143 | < 2e -16 *** | |
| AT | .1.992595 | 0. | 017794 | -111.980 | < 2e -16 *** | |
| V | -0.229235 | 0. | 008479 | -27.034 | < 2e -16 *** | |
| AP | 0.052886 | 0. | 010946 | 4.832 | 1.38e – 06 *** | |
| RH | -0.158685 | 0. | 004837 | -32.803 | < 2e -16 *** |
Signif. codes:
0 ‘ *** ‘
0.001 ‘ ** ‘
0.01 ‘ * ‘
0.05 ‘ . ‘
0.1 ‘ ‘
1
Residual standard error: 4.453 on 6688 degrees of freedom
Multiple R-squared: 0.9312, Adjusted R-squared: 0.9312
F-statistic: 2.264e+04 on 4 and 6688 DF, p-value: < 2.2e-16
// distancia de Cook
In [ ] : powerplant test$pe_est<-predict (model_powerplant_clean, powerplant.test)
plot(powerplant.test$PE, (powerplant, test$PE-powerplant.test$pe_est))
sqrt (mean ( (powerplant.test$PE-powerplant-test$pe_est)^2))
myrsquared (powerplant.test$PE, powerplant.testspe_est)El resultado:
4.64242613613001
0.927834557278113
La gráfica quedaría más o menos así:
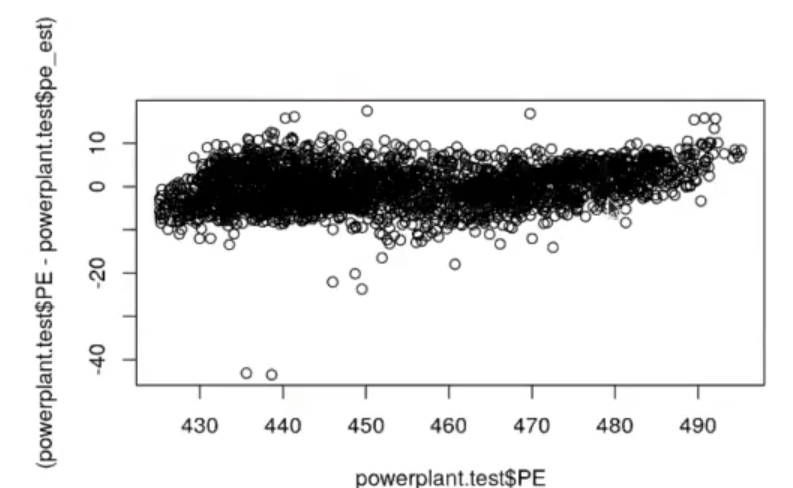
Si comparamos el segundo modelo con el primero, básicamente no ha cambiado nada. Sin embargo, debes fijarte en cómo se desenvuelven los residuos entre un modelo y otro para saber si es una mejor o una peor opción.
Como hemos visto, la distancia de Cook puede ser muy útil en análisis estadísticos en Big Data, aunque esto dependerá mucho de qué necesites. Para adentrarte más en estos conocimientos, te recomendamos seguir nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en donde aprenderás todo lo necesario para ser el mejor profesional. Tendrás a profesores que te guiarán en todo el camino y, en poco tiempo, podrás abrir las puertas del mercado laboral IT. ¡Solicita más información y cambia tu vida!











