¿Qué es la optimización en data mining?

La optimización en data mining consiste en encontrar el mínimo o máximo de una función. Para todos los ejemplos de este artículo vamos a suponer que buscamos el mínimo de una función.

Dada una función f(X), donde X puede ser una constante, un vector o una matriz, el objetivo es encontrar un valor de X que se garantice.

¿En qué consiste la optimización en data mining?

La optimización en data mining es la selección del mejor elemento basado en un criterio particular de un conjunto de alternativas disponibles.

La optimización en data mining implica determinar los mejores valores disponibles de la función objetivo en un dominio definido junto con una variedad de funciones objetivo de diferentes tipos.

A modo de ejemplo

Para que quede más claro el funcionamiento de la optimización en data mining, te ponemos un ejemplo. Vamos a intentar minimizar esta curva:

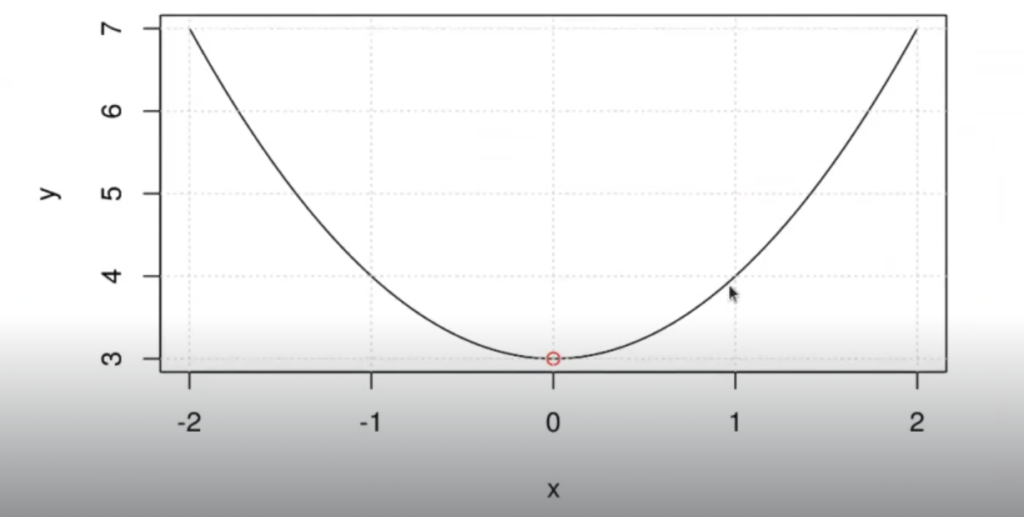
Esta es una parábola de f(x) = x² +3

Así pues:

f(x) = x² +3:

x= argminer (f(x))

x= argmine (x)=0

f(x) = f(0)=0+3=3

Aquí el mínimo está en 0 y es un valor igual a 3.

In [ ]: options (repr.plot.height=4, repr.plot.width=6, repr.plot.res 300)

myfunc <- function (x) { x^2+3 }

x<-seq(-2,2, length.out 100)
y<-myfunc(x)

plot(x,y,t="l")
points (0,3,col="red")
grid()

¿Qué queremos optimizar?

Lo que buscamos con la optimización en data mining es minimizar la función de error.

Todos los algoritmos que usemos van a tener una función de error que va a medir cómo se ajusta nuestra curva de predicción a la curva real. Es lo que en inglés se conoce como curve-fitting.

El objetivo de esa función de error es saber cuánto se equivoca el algoritmo en su decisión. Siempre vamos a tratar de minimizar el valor de esa función de error cambiando los parámetros necesarios.

En la regresión lineal, la función de error es el error cuadrático promedio.

Imagina que nuestra función fuera la siguiente:

y = a . x + b

Lo que haremos será intentar minimizar el margen de error entre el valor predicho (a.x_real+b) y el valor real (y_real).

Todos los problemas aprendizaje son formas más o menos avanzadas de ajuste de curvas

¿Cómo encontramos el mínimo de una función?

En los procesos de optimización en data mining encontraremos el mínimo de la función de forma iterativa. Es decir, inyectando en nuestro modelo un valor distinto para ver qué valor tenemos en la salida. En función de los datos que metemos en la entrada, vemos cuál es la salida que tiene un valor más bajo.

Al ser un proceso iterativo, tenemos que garantizar convergencia, es decir, dado un número suficientemente grande de iteraciones nuestro proceso encontrará el mínimo.

En algunos casos muy contados podemos saltar directamente al mínimo, pero por lo general este no será el caso.

Ejemplo 1:

1. x_0 <- Asignamos un valor x al azar.
2. x_new <- Elegimos otro valor de x próximo a x_0 al azar.
3. Si f(x_new)<f(x_8) entonces x_0 <- x new_.
4. Repetimos desde 2 un número N de veces.

In [2]: x_0 <- runif(1,-2,2)
hiperparametro <- 2

In [ ]: plot(x,y,t="l")
grid()
if (myfunc(x_new) < myfunc(x_0)){
      x_0 <- x_new
}
points (x_new,myfunc(x_new),col="blue")
points (x_0,myfunc(x_0),col="red",pch='x')

In [ ]: x_0 <- runif(1,-10,10)
hiperparametro <- 2

x_historico <- c()
for (i in 1:20) {
         x_new <- rnorm(1,mean=x_0,sd= hiperparametro)
         if (myfunc(x_new) < myfunc(x_0)){
             x_0<- x_new
         }
         x_historico<-c(x_historico, x_0)
}
plot(x_historico, t="o")
grid()

points(x_new,myfunc(x_new),col='blue')
points(x_0,myfunc(x_0),col="red",pch='x')

Vamos probando números al azar para ver qué arrojan los resultados. Si el número nuevo está más cerca del mínimo que su predecesor, ese será el que usaremos:

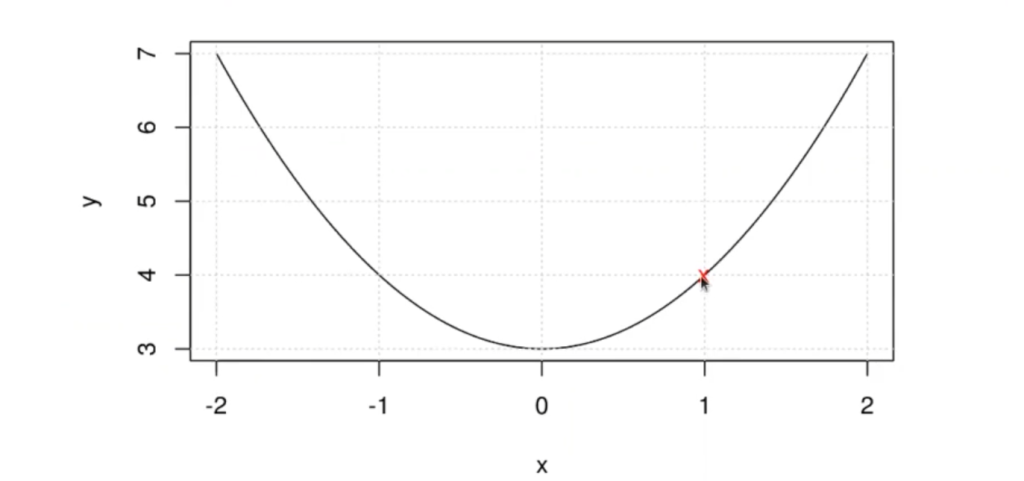
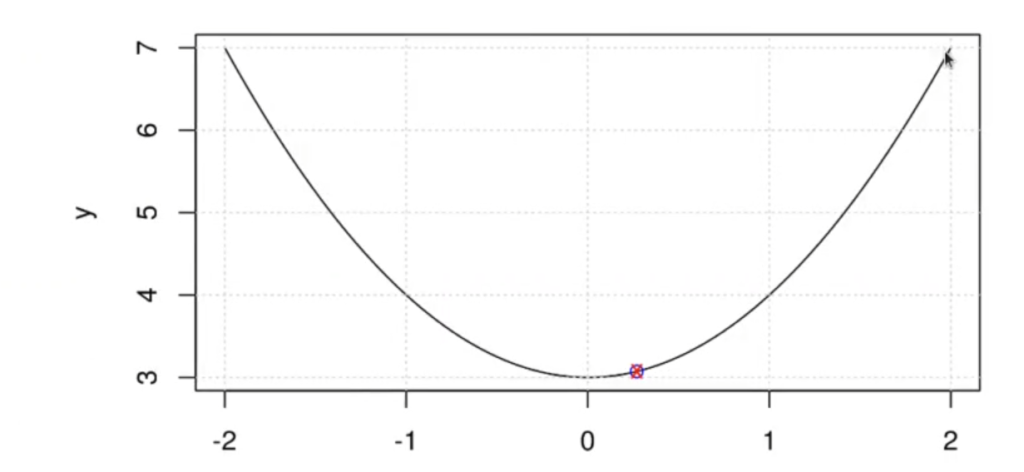
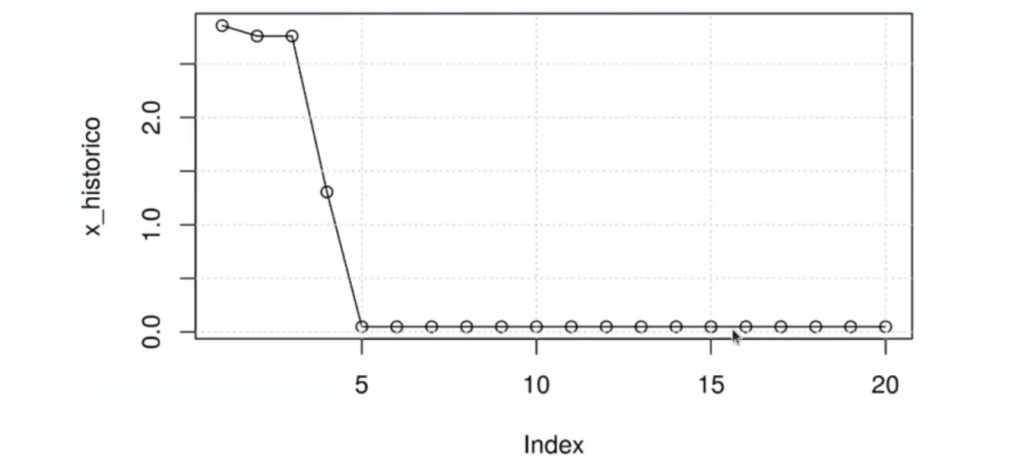
Este método es muy poco práctico ya que utiliza técnicas de data mining obsoletas, como lo es el hecho de ir proponiendo cantidades de datos sin sentido y esperar a que algo funcione, sin hacer una toma de decisiones óptima y adecuada. Esto es un mal negocio y no nos provee de herramientas fundamentales y necesarias en el mundo del Big Data, la inteligencia artificial y en especial de la minería de datos.

Actualmente, existe otro método más óptimo para realizar este tipo de predicciones, que incluye los hiperparámetros y los deltas.

Hay muchísimos aspectos involucrados en el análisis predictivo y, para especializarte en ello, no vas a necesitar solo la programación, sino también la estadística, las matemáticas y otras áreas afines que van a permitirte entender todos los conceptos que conllevan los procesos de optimización en data mining.

Recuerda que desde Keepcoding te ofrecemos acompañamiento por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el que aprenderás todo lo necesario para poder incursionar en el mercado laboral de manera rápida. ¡En tan solo nueve meses serás un experto y te impulsarás en el mundo del Big Data!