¿Qué es la transformación de variables en R?

¿Sabes qué es la transformación de variables en R? ¡Sigue leyendo este artículo y descúbrelo!

Transformación de variables en R

A veces se transforma la variable para conseguir que su distribución siga una normal y/o varianza constante. Una de las técnicas consiste en buscar el parámetro λ, que maximiza el estimador de máxima verosimilitud:

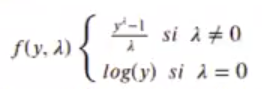
Existen distintas variaciones de la fórmula utilizando la función, pero básicamente todas son lo mismo:

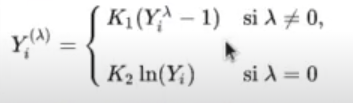
Existen distintas variaciones de la fórmula, pero básicamente todas son equivalentes.

Esta transformación logarítmica se suele conocer como la transformación box-cox. Funciona para valores estrictamente positivos.

Ejemplo de transformación de variables en R

Para entender mejor en qué consiste la transformación box-cox, vamos a tomar un ejemplo de una central eléctrica.

En este ejercicio de transformación de variables en R estamos utilizando la función que utiliza la librería de R. Existen distintas versiones de esta función en R, tienes que mirar bien la librería que uses.

Utilizando la función, se intentan calcular para distintos valores de lambda cuál es el valor que más se acerca a una gaussiana, que deja los datos más parecidos a este tipo de distribución.

Pasamos el modelo:

In [52] : library(MASS)
bx <- boxcox (model_powerplant, lambda = seq (-5, 1, length.out = 100))

Y el resultado es este:

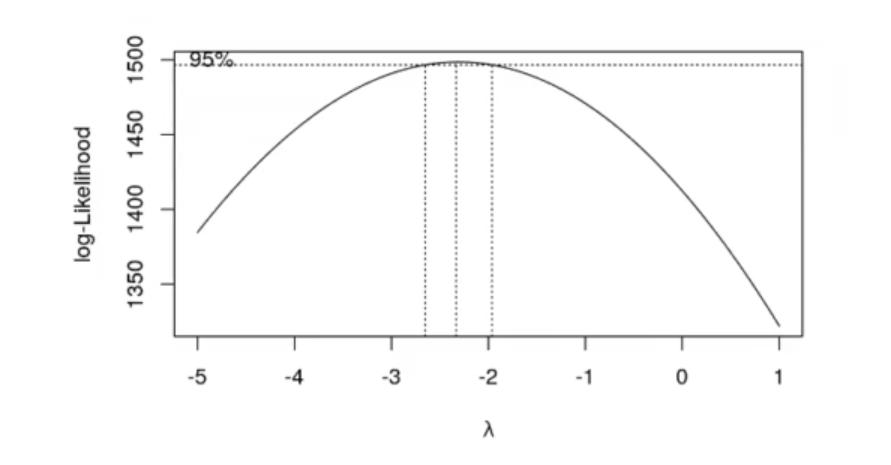
Por ejemplo, para el ejercicio de preprocesado en R aplicando regresión lineal que hicimos en un artículo anterior, basamos el modelo. Al mismo tiempo, en este nuevo ejercicio de transformación de variables en R, nos dice que si cogemos un lambda de -1 o más o menos este valor vamos a tener una distribución que siga ligeramente más una distribución normal:

In [53] : l <- bx$x [which.max (bx$y)]
my_transform <- function (y, 1) {
(y ^ l -1) / 1
}

-2.333333333333333

Podemos observar que, efectivamente, el resultado de esa distribución es -2.333333333333333.

Al final, bx es un vector:

Es una lista que tiene los valores de X e Y y que permiten calcular el gráfico anterior sobre transformación de variables en R. ¿Qué nos está representando este gráfico? Lo que muestra es cómo definir con una gaussiana nuestros datos en función del parámetro lambda. Si lambda es 0, estamos usando un logaritmo; es decir, cuando lambda tiende a 0, vale el logaritmo mediano.

Nos fijamos en que es constante la gráfica, porque si lambda es 0, el numerador está indeterminado, porque está dividiendo 0 entre 0, pero tiende al logaritmo.

Siguiendo con el ejercicio de transformación de variables en R, lo que tenemos que hacer, acto seguido, es crear una función que nos haga esta transformada (y ^ l -1) y transformar el PE (potencia de salida) con la función my_transform. Luego, volvemos a calcular el modelo en el que, en lugar de predecir el PE, ahora predecimos el PE transformado (PE_tr) para train. Esta transformación la aplicamos a los datos de train:

In [56] : powerplant_transformed.train <- powerplant.train
powerplant_transformed.train$PE_tr <- my_transform (powerplant.train$PE, l)
model_powerplant_tr <- lm (PE_tr ~ AT + V + AP + RH, data = powerplant_transformed.train)

In [57] : par (mfrow = c(1, 2))
qqnorm (y = model_powerplant$residuals, cex = 0.1)
qqline (y = model_powerplant$residuals, cex = 0.1, col = "red")

qqnorm (y = model_powerplant_tr$residuals, cex = 0.1)
qqline (y = model_powerplant_tr$residuals, cex = 0.1, col = "red")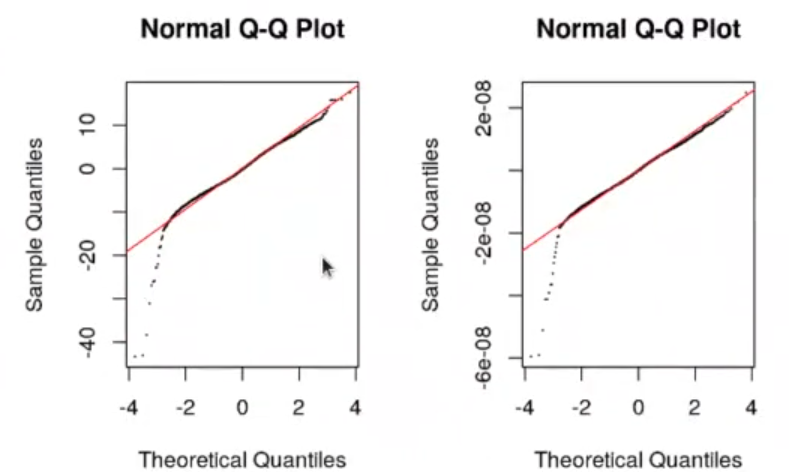

Aquí miramos los residuos con un Q-Q plot, aunque no hay muchísimas diferencias, ya que los resultados siguen casi una distribución normal.

También vemos los resultados en la primera gráfica, que son los datos originales de los residuos. En la segunda, vemos los resultados de los datos ya transformados y, en este último caso, los registros tienden a seguir un poco una distribución más normal.

Si bien es cierto que en el inicio hay unos puntos que son incongruentes, existen otras regiones en donde sí se ven más pegados a la línea.

De todo esto podemos concluir que con esta transformación de variables en R mejoraron un poquito los residuos.

En este caso, la transformación de variables en R no mejora el R² ni el R^2.

¿Quieres saber más?

Recuerda que si quieres seguir aprendiendo sobre esta temática, tienes a los mejores profesionales para acompañarte en tu proceso en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva, en poco tiempo podrás instruirte en todo lo necesario para incursionar rápidamente en el mundo laboral. ¡Anímate a impulsar tu carrera y solicita información!