PCA en estadística: Qué es y cómo calcularlo

¿Alguna vez te has sentido abrumado al trabajar con grandes volúmenes de datos y no saber por dónde empezar? No te preocupes, a mí también me ha pasado muchas veces. Enfrentarnos a un dataset enorme puede ser muy complicado, sobre todo, si eres principiante. En mi caso, lo que me salvó la vida fue descubrir el PCA en estadística, ya que me ayudó a simplificar todo ese caos y me mostró cómo extraer lo realmente importante de los datos.

En este artículo, quiero enseñarte qué es el PCA en estadística, para qué sirve y cómo puedes aplicarlo, incluso si estás dando tus primeros pasos en el análisis de datos. 

¿Qué es el PCA en estadística?

El PCA, por sus siglas en inglés Principal Component Analysis, es una técnica estadística que se utiliza para reducir la dimensionalidad de los datos. Pero, ¿qué significa eso? Imagínate que tienes un gran tablero lleno de post-its, donde cada color y forma representan variables diferentes. El PCA te ayuda a reorganizar todo ese caos para enfocarte solo en las combinaciones más relevantes.

En términos más técnicos, el PCA transforma tus variables originales en un conjunto más pequeño de variables llamadas componentes principales, que capturan la mayor parte de la variabilidad de tus datos. Es como condensar la información de un libro en un resumen, pero manteniendo lo esencial.

¿Para qué sirve el PCA en estadística?

El PCA en estadística es una herramienta realmente útil, pues tiene usos prácticos muy potentes. Veamos algunos de ellos:

1. Reducción de dimensionalidad: Simplifica datasets complejos al reducir el número de variables, facilitando su análisis.
2. Visualización de datos: Ayuda a representar datos multidimensionales en gráficos de 2D o 3D para identificar patrones.
3. Eliminación de ruido: Al centrarse en los componentes principales, se filtran las variables menos relevantes o redundantes.
4. Preparación de datos para modelos predictivos: Hace que los modelos sean más eficientes al reducir la complejidad sin perder información crucial.

Por ejemplo, en un estudio sobre clientes de un supermercado, el PCA podría ayudarte a identificar patrones de compra sin tener que analizar cada variable individualmente, como edad, ingresos o frecuencia de visitas.

Paso a paso para realizar un PCA manualmente

Es cierto que las herramientas automatizadas como Python y R hacen que el PCA en estadística sea mucho más sencillo, pero si entiendes cómo funciona esta técnica, tendrás un control mucho mayor sobre tus datos. Por eso, quiero explicarte a continuación cómo puedes realizarlo de forma manual.

Estandarización de los datos

Primero, necesitas normalizar tus datos para que todas las variables estén en la misma escala. Esto se hace restando la media de cada variable y dividiendo entre su desviación estándar.

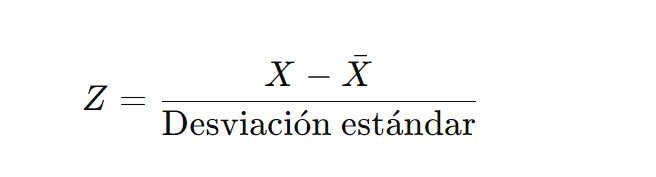
Construcción de la matriz de covarianza

La matriz de covarianza muestra cómo varían juntas las diferentes variables del dataset.

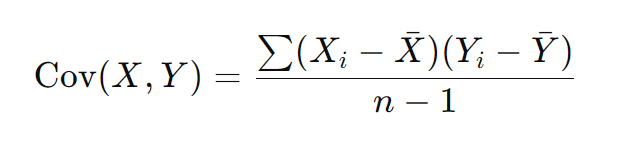
Cálculo de los valores y vectores propios

Ahora, debes calcular los valores propios (eigenvalues) y los vectores propios (eigenvectors) de la matriz de covarianza usando álgebra lineal. Estos te indican la magnitud y dirección de la variabilidad en los datos.

Selección de componentes principales

Ordena los valores propios de mayor a menor y selecciona los componentes principales que expliquen un porcentaje significativo de la varianza total, normalmente entre el 70% y el 90%.

Proyección de los datos

Por último, proyecta tus datos originales en los componentes principales seleccionados para obtener el nuevo dataset reducido.

Paso a paso para realizar un PCA en Python

Ahora sí, quiero explicarte cómo puedes llevar este proceso al código. Para esto, usar Python y librerías como Scikit-learn te facilitará la vida. Veamos un ejemplo sencillo:

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import pandas as pd

# Supongamos que tienes un DataFrame llamado "datos"
scaler = StandardScaler()
datos_escalados = scaler.fit_transform(datos)

# Aplicamos PCA
pca = PCA(n_components=2)  # Reducimos a 2 componentes
componentes = pca.fit_transform(datos_escalados)

# Visualizamos la importancia de cada componente
print(pca.explained_variance_ratio_)

Este código realiza todos los pasos clave del PCA: normalización, selección de componentes y cálculo de la variabilidad explicada. Una vez que lo domines, estarás listo para aplicarlo a proyectos reales.

Implementación manual en Python

Continuemos con otro ejemplo. Supongamos que tienes un dataset con las siguientes variables:

En Python, tendríamos que ejecutar el código de la siguiente manera:

import numpy as np

# Paso 1: Estandarización de los datos
datos = np.array([[4.0, 1.0], [2.0, 3.0], [3.0, 2.0]])
media = np.mean(datos, axis=0)
desviacion = np.std(datos, axis=0)
datos_estandarizados = (datos - media) / desviacion

# Paso 2: Matriz de covarianza
matriz_cov = np.cov(datos_estandarizados.T)

# Paso 3: Cálculo de valores y vectores propios
valores_propios, vectores_propios = np.linalg.eig(matriz_cov)

# Paso 4: Selección de componentes principales
idx = valores_propios.argsort()[::-1]  # Ordenar de mayor a menor
valores_propios = valores_propios[idx]
vectores_propios = vectores_propios[:, idx]

# Paso 5: Proyección de los datos
datos_reducidos = np.dot(datos_estandarizados, vectores_propios[:, :2])

print("Datos reducidos:\n", datos_reducidos)

Este código realiza cada paso manualmente, desde la estandarización hasta la proyección en los componentes principales. Como resultado, tendremos un dataset reducido que captura la mayor parte de la variabilidad.

Finalmente, puedo decirte que aprender a usar el PCA en estadística es como enfocar una cámara para capturar un panorama amplio en una imagen clara y precisa. Así que ahora sabes que con esta herramienta, puedes analizar datasets más grandes y complejos, resumiendo lo esencial sin perder la información más importante.

Si quieres continuar aprendiendo sobre las herramientas y tecnologías más avanzadas y demandadas en la actualidad de big data y data science, no lo pienses más y únete a nuestro Bootcamp en Big Data, Machine Learning e IA. Esta es la oportunidad perfecta para que empieces una nueva carrera en una de las áreas más demandadas del sector IT.

¿Qué estás esperando para darle un nuevo rumbo a tu vida?