¿Qué es PCA en estadística?

El PCA en estadística, sigla que significa Principal Component Analysis y cuya traducción quiere decir «Análisis de componentes principales ACP», es un algoritmo de machine learning no supervisado sumamente famoso para diferentes tareas, como análisis exploratorio de un conjunto de datos o para reducir la dimensionalidad. También sirve para encontrar secuencias de una combinación lineal de variables, entre otras cosas.

Ejemplo de PCA en estadística

Una vez vista la pca definicion , analicemos un ejemplo:

En este caso vamos a realizar una transformación de nuestros datos originales en un nuevo espacio vectorial. Nos interesa encontrar la dirección de máxima variabilidad de los datos para, sobre esa dirección (vector), proyectar nuestros datos sobre una base ortonormal.

p→ = Σ a_i, u_i→

Los autovectores de la matriz de covarianza de nuestros datos o A¹ – A nos proporcionan esa base vectorial sobre la cual proyectar nuestros datos.

• Cuanto mayor sea el autovalor, más importancia y más varianza tendrá la prospección de los datos sobre el autovector correspondiente.
• Los autovectores de la matriz de covarianza de A coinciden con la diagonal de la matriz de covarianza de la proyección de A sobre la base vectorial de autovectores.

#PCA en estadística
# pca ml
M <- matrix (c (mydata$x1, mydata$x2), ncol = 2)
eigv <- eigen (t (M %>% M) $vector)
eigen (t (M) %>% M)
eigen (cov (M))

ggplot (mydata, aes (x = x1, y = x2)) + geom_point (size = 0.5) + 
geom_abline (intercept = 0, slope = eigv [2, 1] / eigv [1, 1], color = "red") + 
geom_abline (intercept = 0, slope = eigv [2, 2] / eigv [1, 2], color = "blue") + 
xlim (c (-15, 15)) + ylim (c (-15, 15)) + 
theme_bw () + coord_fixed ()

eigen () descomposition
$values

[1] 3678.4596 470.3199

$vectors

	[ , 1 ]	[ , 2 ]
[ , 1 ]	-0.8910839	0.4538385
[ , 2 ]	-0.4538385	-0.8910839

eigen () descomposition

$values

[1] 24.670594 3.142724

$vectors

	[ , 1 ]	[ , 2 ]
[ , 1 ]	-0.8914069	0.4532038
[ , 2 ]	-0.4532038	-0.8914069

Para calcular el PCA en estadística, partimos de una nube de puntos como la que vemos a continuación:

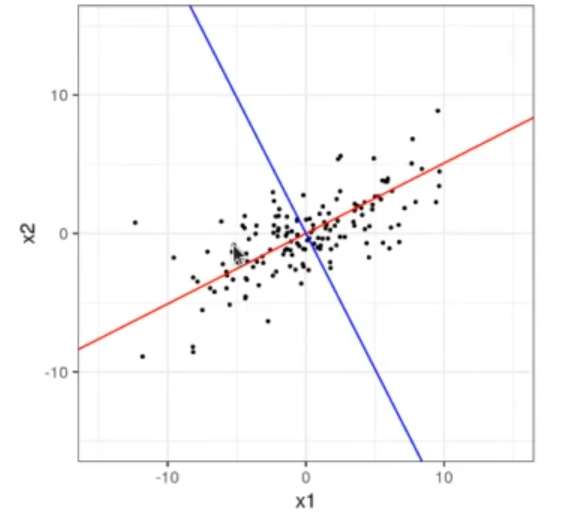
Aquí hemos puesto que nuestros datos están divididos en dos dimensiones. Si observamos la correlación, nos damos cuenta de que hay una correlación positiva.

Si queremos que x1 y x2 no estén correlacionadas, tenemos que girar la cruz formada por la línea roja y la línea azul. ¿Cómo lo hacemos? Observa:

#PCA en estadística
# pca python
mydata_rot <- data.frame (x1 = M %% eigv [ , 1 ], x2 = M %*% eigv [ , 2 ])

ggplot (mydata_rot, aes (x = x1, y = x2)) + geom_point (size = 0.5) +
geom_hline (yintercept = 0, color = "red") +
geom_vline (xintercept = 0, color = "blue") +
xlim (c (-15, 15)) + ylim (c (-15, 15)) +
theme_bw ()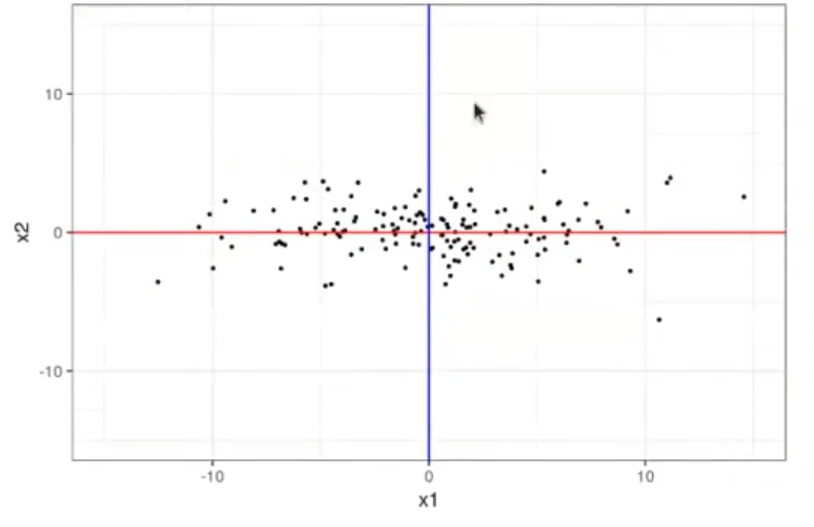

Los ejes de las líneas rojas y azul van a venir dados por los autovectores. Los autovectores nos dicen hacia dónde apunta la mayor variación de los datos. De esta forma, pudimos llegar a una correlación 0 entre x1 y x2.

#PCA en estadística
# Los autovalores de la matriz de covarianza de A coinciden con
# la diagonal de la matriz de covarianza de la proyección de A sobre la base vectorial de autovectores
var (mydata_rot)
eigen (var (M)) $values

	x1	x2
x1	24.68058345	-0.01533166
x2	-0.01533166	3.14273523

24.6705943659864 3.14272430937977

Diferencias entre PCA y regresión lineal

La regresión lineal busca minimizar el error cuadrático medio:

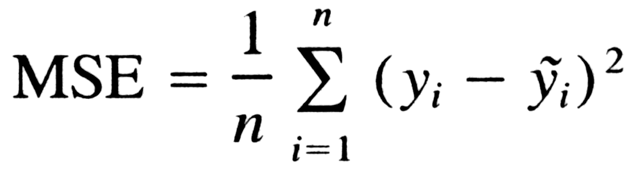
En PCA buscamos maximizar la proyección de nuestros datos sobre la nueva base vectorial, de forma que el error sobre esa proyección sea el mínimo posible.

En la siguiente figura se ve claro:

• El PCA busca minimizar la distancia de los puntos a la linea roja de forma perpendicular (línea discontinua).
• La regresión lineal busca minimizar la distancia de los puntos a la línea verde de forma vertical (línea discontinua).

#PCA en estadística / linear model
mydata_pcal <- as.data.frame (x = matrix (mydata_rot$x1, ncol = 1) %*% t (eigv [ , 1 ]))
colnames (mydata_pcal) <- c ("xlpca", "x2pca")
mydata_total <- cbind (mydata, mydata_pcal)

linear_model <- lm (mydata, formula = x2 ~ 1)
mydata_total$x2lm <- predict (linear_model, mydata)

ggplot (mydata_total [1 : 10, ], aes (x = x1, y = x2)) +
geom_point (aes (x = x1pca, y = x2pca), color = "red") +
geom_abline (intercept = 0, slope = eigv [2, 1] / eigv [1, 1], color = "red") +
#geom_abline (intercept = 0, slope = eigv [2, 2] / eigv [1, 2], color = "red") +
geom_segment (aes (x = x1, y = x2, xend = x1pca, yend = x2pca), color = "red", linetype = "dashed") +
geom_abline (intercept = linearl_model$coefficients [1], slope = linear_model$coefficients [2], color = "#00FF88") +
geom_segment (aes (x = x1, y = x2, xend = x1, yend = x2lm), color = "00FF88", linetype = "dashed"), +
geom_point (size = 1) +
xlim (c (-12, 12)) + ylim (c (-9, 9)) + 
theme_bw ()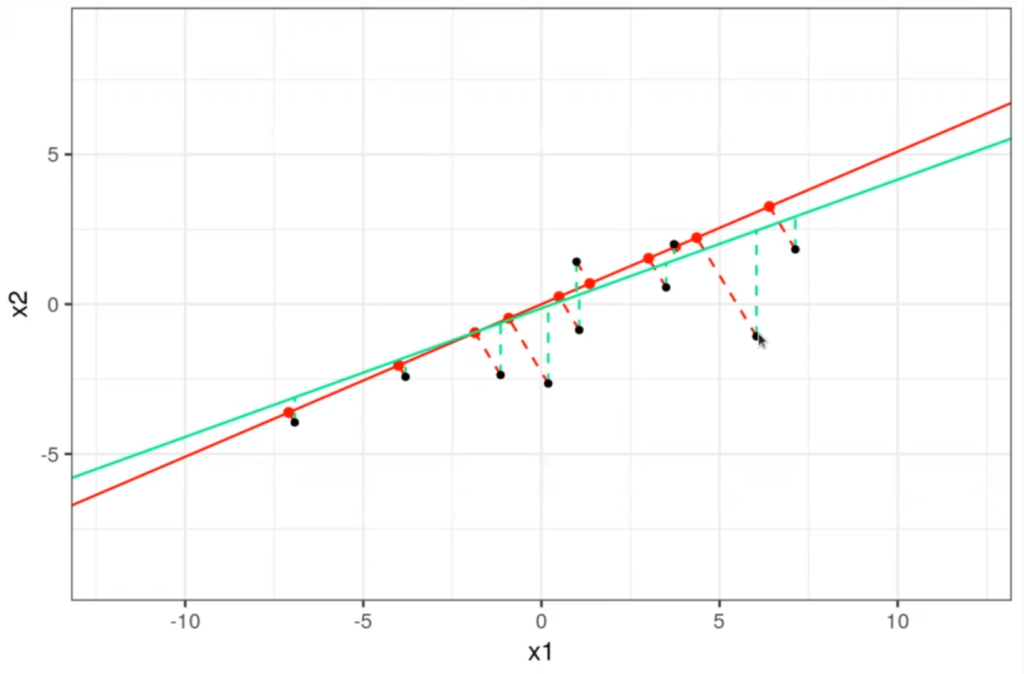

¿Qué sigue?

Ahora que sabemos qué es el PCA en estadística, podemos seguir aprendiendo sobre otras temáticas importantes para el minado de datos, como la regresión lineal y logística.

Si no tienes ni idea de qué es esto, tenemos la solución para ti: con nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp podrás adquirir todos los conocimientos necesarios para incursionar rápidamente en el mundo laboral. ¡Solicita más información ahora y empieza a cambiar tu vida!