¿Alguna vez te has topado con un polinomio que parece complicado? Aprender a simplificar polinomios puede ser una habilidad muy útil en matemáticas, por eso hoy queremos mostrarte cómo hacerlo con unos cuantos trucos.
¿Qué es un polinomio?
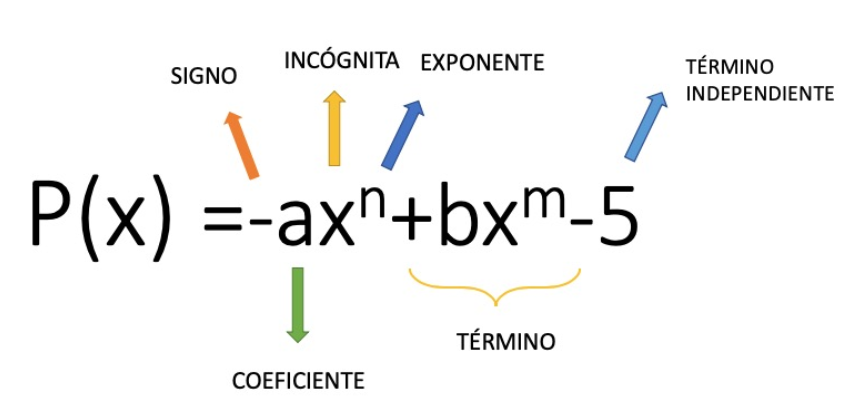
Antes de entrar en materia con el proceso de simplificar polinomios, hagamos una pequeña recapitulación. Un polinomio es una expresión algebraica que está formada por varios términos, cada uno de esos términos es llamado monomio. Los monomios pueden estar compuestos por variables, números y exponentes.
Por ejemplo, este es un polinomio:
3x^2 + 2x – 5
Aquí, los términos son 3x², 2x y -5.
Simplificar un polinomio te permite convertir una expresión complicada en algo más manejable, con lo que podrás ahorrar tiempo en diferentes operaciones.
Nota: Recuerda que, en matemáticas, el exponente puede verse representado de dos formas: 1. 3x^2 o 2. 3x²
Términos semejantes: el truco para simplificar polinomios
Uno de los conceptos básicos para simplificar polinomios es identificar términos semejantes dentro de las ecuaciones polinómicas. Pero, ¿qué son exactamente? Los términos semejantes son aquellos que tienen la misma variable y el mismo exponente. Por ejemplo, en el polinomio:
4x^2 + 3x^2 – 2x + 5
Los términos semejantes son 4x² y 3x², porque ambos tienen la misma variable (x) y el mismo exponente (2). Aquí es donde empieza la magia de la simplificación.
¿Cómo identificar términos semejantes?
Es sencillo: solo tienes que fijarte en los términos que comparten la misma variable y el mismo exponente. Si no tienen el mismo exponente, no los puedes combinar.
Ejemplo:
Polinomio original:
5x^3 + 2x^2 + 3x^3 – x^2 + 7
Para simplificarlo, identifica los términos semejantes:
- 5x³ y 3x³
- 2x² y -x²
Ahora, sumas o restas los coeficientes:
(5x^3 + 3x^3) + (2x^2 – x^2) + 7 = 8x^3 + x^2 + 7
Simplificación de polinomios: paso a paso
Ahora que tienes clara la idea de términos semejantes, vamos a ver un truco sencillo que te ayudará a simplificar polinomios de manera eficiente.
- Elimina paréntesis si los hay
Si tu polinomio tiene paréntesis, lo primero que debes hacer es eliminarlos utilizando la propiedad distributiva.
Ejemplo:
2(x^2 + 3x) + 4x
Distribuye el 2:
2x^2 + 6x + 4x
- Agrupa los términos semejantes
Una vez que hayas eliminado los paréntesis, es momento de agrupar los términos semejantes. Recuerda que para poder sumar o restar términos, deben tener la misma variable y el mismo exponente.
Ejemplo:
2x^2 + 6x + 4x = 2x^2 + (6x + 4x)
- Suma o resta los coeficientes
En este paso, simplemente suma o resta los coeficientes de los términos semejantes que has agrupado.
Ejemplo:
2x^2 + (6x + 4x) = 2x^2 + 10x
¿Qué pasa si hay más de una variable?
Cuando trabajas con polinomios que tienen más de una variable, el proceso es el mismo. Solo debes asegurarte de que tanto las variables como sus exponentes sean iguales para agrupar los términos.
Ejemplo:
3xy + 2xy – 5x^2 + 4x^2
Agrupas los términos semejantes:
(3xy + 2xy) + (-5x^2 + 4x^2)
Y luego sumas o restas los coeficientes:
5xy – x^2
Veamos un ejemplo
Ahora veamos un ejemplo completo del proceso de simplificar polinomios, para entender mejor cómo funciona:
Polinomio original:
4x^2 + 3x – 2x^2 + 7 – 6x
- Agrupa los términos semejantes
- 4x² y -2x²
- 3x y -6x
- 7 no tiene términos semejantes.
- Suma los coeficientes
(4x^2 – 2x^2) + (3x – 6x) + 7 = 2x^2 – 3x + 7
Este es el polinomio simplificado.
Preguntas frecuentes
- ¿Cuáles son las reglas básicas para simplificar polinomios?: Las reglas son simples: agrupa términos semejantes y luego suma o resta sus coeficientes. Utiliza la propiedad distributiva si es necesario para eliminar paréntesis y facilitar la agrupación. También puedes usar una calculadora para simplificar expresiones.
- ¿Por qué es importante simplificar polinomios?: Simplificar polinomios es importante porque te permite trabajar con expresiones algebraicas de forma más práctica.
- ¿Qué pasa si un polinomio tiene fracciones?: En ese caso, simplemente aplica las reglas de suma y resta de fracciones. Agrupa los términos semejantes y luego opera con los coeficientes fraccionarios.
Si quieres seguir aprendiendo sobre matemáticas y su uso en programación, puedes unirte a nosotros en el bootcamp en big data y machine learning. Allí aprenderemos la incidencia que tienen las matemáticas y sus áreas derivadas, en los procesos llevados a cabo en Big data. ¡Apúntate ahora y comienza tu transformación profesional!











