¿Qué es una matriz?

¿Cómo definirías una matriz? A rasgos generales, una matriz es una serie de números distribuidos en filas y columnas. Las matrices están intrínsecamente relacionadas con las transformaciones lineales, las cuales son la base del perceptrón, la unidad básica de las redes neuronales.

Definición de matriz

Observemos y pensemos en la siguiente imagen:

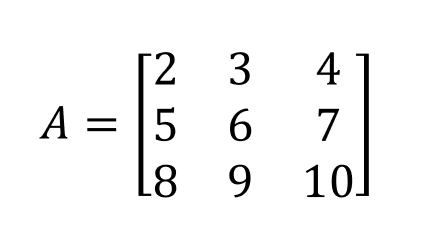
Una matriz viene denotada por sus filas y sus columnas. Hay distintas notaciones; en nuestro caso lo haremos del siguiente modo:

• Las filas corresponderán a la letra m.
• Las columnas corresponderán a la letra n.

¿Matrices y vectores?

Recordemos cuando hemos hablado de los vectores. Tenemos por ejemplo el siguiente vector → [3, 2, 1, 5]. Este vector tendría 4 componentes y pertenecería al espacio R4 (v ∈ R⁴).

En las matrices funciona igual. Veamos la siguiente matriz:

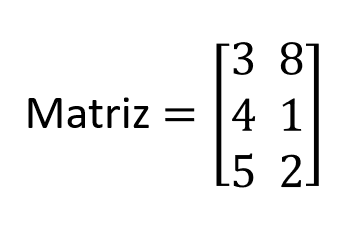
Esta matriz sería m x n. Ya habíamos dicho que m son las filas y n las columnas, de modo que la matriz quedaría denotada así: m x n → 3 x 2. De manera que esta matriz, llamémosla A, corresponde al espacio 3 x 2 (A ∈ R^{3 x 2}).

Ahora bien, si esto, en vez de ponerlo con un ejemplo, lo desarrolláramos, podríamos decir que:

Matrices → vectores

A (m x n) ∈ R^{(m x n)}

No obstante, si a la matriz que tenemos le elimináramos la última fila, correspondiente a los números 5 y 2, esta quedaría ya no de 3×2, sino de 2×2. Ahora quitemos otra fila, ¿ves hacia dónde vamos con esto? Esta no quedaría de 2×2, sino de 1×2, por lo que aquí ya tenemos claro que el resultado sería que la matriz queda exactamente igual que un vector.

El vector no es más que haber convertido una o varias matrices a una fila, en donde estamos modificando el valor de m a medida que suprimimos filas (tal y como acabamos de ver en el ejemplo anterior), hasta obviarlo (ya que no se elimina).

¿Tensores → Matrices → Vectores?

Si en vez de ir hacia la derecha (matrices → vectores), vamos hacia la derecha (tensores → matrices → vectores), tendríamos los tensores.

Los tensores no son más que una secuencia de números ordenados de tal forma que tienen más de dos dimensiones. Los tensores los podemos denotar como d x n x m, así pues: d x n x m R ^{d x n x m}.

Entonces, cuando al tensor le vamos quitando componentes (igual que hemos hecho con la matriz) hasta que el valor de d se modifica tanto que ya podemos obviarlo, la fórmula quedaría n x m, como una matriz.

Ya sabemos cómo escribir matrices. También sabemos que estas pueden tener diversos componentes; ahora bien, ¿podrías establecer alguna relación entre las matrices y la transformación lineal?

Ahora es tu turno

Veamos si puedes resolver algunos ejercicios:

1. ¿Crees que podrías decirnos cuáles son las dimensiones de las siguientes matrices?

2. ¿Podrías decirnos cómo armaríamos una matriz de 2 x 3 con D_{1, 2} = 6?

Veamos las soluciones:

1. Respuestas:
   • La matriz E tendría dimensiones de 4×4
   • La matriz F tendría dimensiones de 5×5
   • La matriz G tendría dimensiones de 3×10
2. Respuestas:
   • D = 2 6 8
     7 -3 1

¿Quieres seguir aprendiendo?

Ahora que, gracias a esta pequeña introducción sobre las matrices y su funcionamiento, has aprendido todo lo necesario sobre una matriz, puedes seguir aprendiendo sobre Big Data para convertirte en un experto en el sector.

Si quieres acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra y de alta intensidad en la que adquirirás, en pocos meses, todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!