¿Qué son las tablas de verdad y cómo aplicarlas en lógica?

Las tablas de verdad son un elemento muy asiduo en lógica proposicional y matemática y se usan para analizar y determinar la veracidad de proposiciones lógicas compuestas.

Fueron creadas por Charles Sanders Peirce Ludwig Wittgenstein y surgieron como un método de análisis semántico con el que se evalúan condiciones de verdad con base en los valores de sus componentes.

Su versatilidad y amplia estructura hacen que sean muy usadas en campos diversos, como la informática, la ingeniería y las matemáticas. Por eso, hoy queremos explicarte qué son las tablas de verdad y cómo aplicarlas en campos como la programación.

¿Qué son las tablas de verdad?

Las tablas de verdad son un formato de representación gráfica en el que se establecen todas las combinaciones posibles de valores de verdad, o sea, verdadero o falso, para las proposiciones simples que componen una proposición compleja. Se aplican en los casos en donde se quiere determinar si una proposición lógica es verdadera en diferentes escenarios.

Por ejemplo, en el caso de que tuviéramos una proposición simple, como A, la tabla de verdad mostrará los valores posibles de verdad, ya sea V – Verdadero o F – Falso. Si existe más de una proposición, las combinaciones de verdad posibles se calculan con la fórmula 2^n, donde n es el número de proposiciones.

Las tablas de verdad en programación se usan para crear condiciones lógicas en estructuras de control como son los if-else. Por ejemplo, cuando evaluamos varias condiciones en un mismo bloque, los operadores lógicos AND y OR, siguen el mismo principio de las tablas de verdad.

¿Cómo funciona una tabla de verdad?

Las tablas de verdad se construyen de la siguiente manera:

1. Columnas: Representan las variables proposicionales simples, como (p), (q), (r), y las operaciones lógicas entre ellas.
2. Filas: Contienen las combinaciones posibles de verdad de las proposiciones simples. Cada fila muestra un caso posible de la evaluación de la proposición compleja.

¿Cómo hacer una tabla de verdad?

Supongamos que tenemos una proposición simple, (p), y queremos construir su tabla de verdad con la operación de negación (¬). Esto significa que invertimos el valor de verdad de (p):

(p)	¬(p)
V	F
F	V

En este caso, si (p) es verdadero, ¬(p) será falso, y viceversa.

Conectores lógicos y su uso en las tablas de verdad

En lógica proposicional usamos conectores lógicos para combinar proposiciones simples y formar proposiciones más complejas. Algunos de los conectores más comunes son:

• Negación (¬): Invierte el valor de verdad de una proposición.
• Conjunción (∧): Es verdadera solo si ambas proposiciones son verdaderas.
• Disyunción (∨): Es verdadera si al menos una de las proposiciones es verdadera.
• Condicional (→): Es falso únicamente cuando el antecedente es verdadero y el consecuente falso.
• Bicondicional (↔): Es verdadera si ambas proposiciones tienen el mismo valor de verdad.

Tipos de tablas de verdad

Conjunción

La conjunción entre dos proposiciones, (p) y (q), es verdadera solo si ambas son verdaderas:

(p)	(q)	(p ∧ q)
V	V	V
V	F	F
F	V	F
F	F	F

Disyunción

La disyunción entre dos proposiciones, (p) y (q), es verdadera si al menos una de ellas es verdadera:

(p)	(q)	(p ∨ q)
V	V	V
V	F	V
F	V	V
F	F	F

Condicional

El condicional es falso solo cuando el antecedente es verdadero y el consecuente es falso:

(p)	(q)	(p → q)
V	V	V
V	F	F
F	V	V
F	F	V

Otras tablas de verdad que podemos encontrar son:

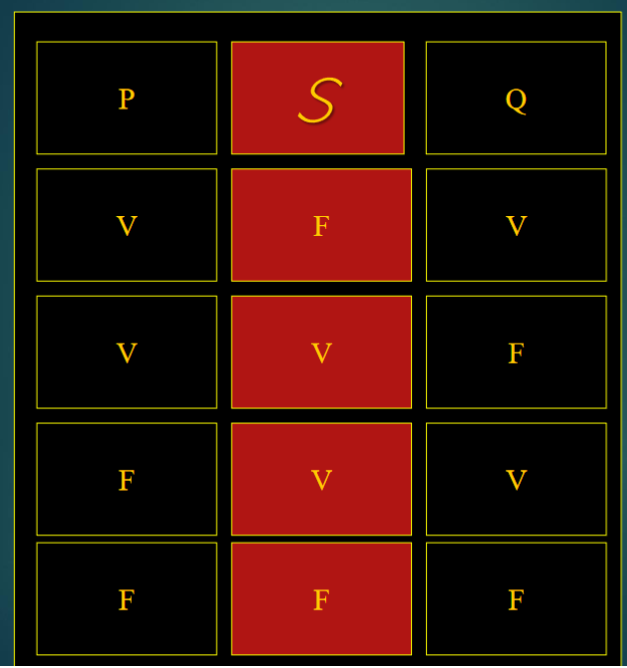
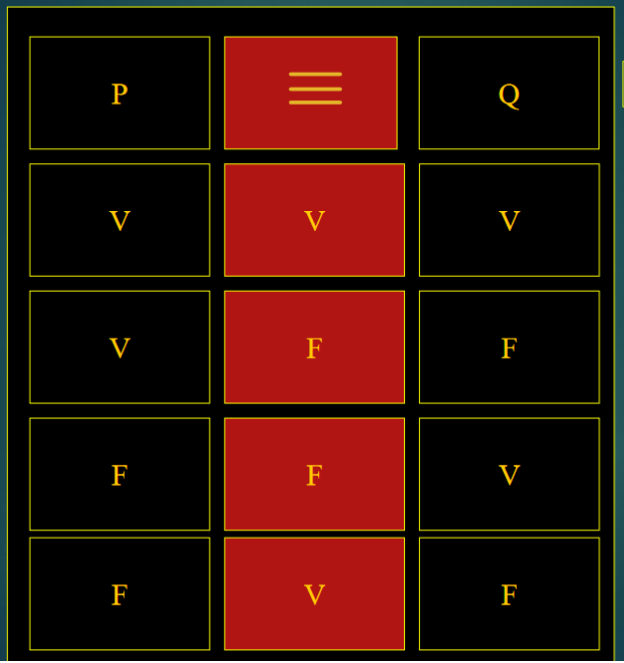
Si te interesó este tema sobre lógica y programación y quieres saber cómo aplicar diferentes conceptos matemáticos en el mundo del desarrollo de software, no dudes en unirte a nuestro bootcamp en programación inicial, con el cual adquirirás todas las herramientas que te llevarán a convertirte en un gran programador y conseguir el trabajo de tus sueños. ¡Apúntate ya y descubre un universo completamente desconocido!