Los autovectores son una característica de la matriz que representa la desviación típica de la muestra de datos en cuanto cambian su dirección, marcada por su correspondiente autovector.
Si ordenamos los autovectores por su valor, veremos que la mayor parte de la variación se encuentra en los primeros autovalores del autovector asociado. El resto aportan cada vez menos información.
Ejemplo de autovectores
Los autovalores y autovectores de una matriz se representan con un sistema de ecuaciones con el que resolvemos el sistema. Estos pueden ayudarnos a entender variaciones del conjunto de datos que hemos obtenido.
Veamos ahora un ejemplo de los autovectores para que quede más claro:
plot (log10 (pr_pics$sdev), t = 'l', ylim = c (0,2))
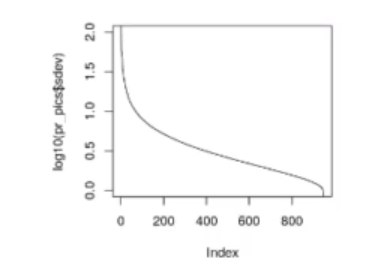
Observamos que con los primeros 5 o 6 componentes principales ya tenemos una gran cantidad de variables.
Para entender bien qué es un componente, veamos lo siguiente.Tenemos una matriz que representa un componente principal en donde si todo es 0, la salida va a ser 0; pero ¿qué ocurre si el primer elemento del componente principal no es 0, sino 1?
t_pic <- matrix (rep (0, ncol (pr_pics$rotation)), nrow = 1) #t_pic [1] <- 1 #t pic[1:50] <- 1 t_pic [100] <- 1 pic_normalizada <- t_pic %>% t (pr_pics$rotation) summary (array(pic_normalizada)) pic_normalizada <- (pic_normalizada - min (pic_normalizada)) pic_normalizada <- pic_normalizada / max (pic_normalizada) plot_row_image (pic_normalizada)

Ya podemos ver que la imagen claramente es una cara. Si, por ejemplo, a los 50 primeros componentes principales les asignamos un valor 1 y al resto 0:

Tenemos, pues, distintas caras que se han ido sobreponiendo.
Una vez que tenemos una imagen transformada con sus componentes principales, podemos borrar los que corresponden a autovalores con menor peso.
De esta forma estaremos perdiendo información, pero la mínima posible, con lo que la reconstrucción posterior de la imagen seguirá siendo posible, aunque con pérdidas.
Se puede demostrar que para las imágenes del conjunto de train, si las pasamos al dominio de PCA, eliminamos los componentes menos importantes y las volvemos a transformar al dominio de las imágenes. Estas habrán sufrido una pérdida de información mínima, es una compresión con pérdidas muy eficiente.
Si utilizamos una imagen de test y aplicamos el mismo proceso, aunque el resultado no será tan bueno, también veremos que es suficientemente bueno. Este método se puede utilizar para comprimir imágenes que comparten características comunes.
# Por motivos didácticos crearemos una función similar a predict:
transform_pca <- function (pca_result = pr_pics, row) {
v <- matrix (row, nrow = 1)
v_normalizada <- (v - pca_result$center) / pca_result$scale
v_normalizada %*% pca_result$rotation
}
# Y una función que haga su inversa:
inv transform_pca <- function (pca_result = pr_pics, row) {
v <- matrix (row, nrow = 1)
pic_normalizada <- v %*% t (pca_result$rotation)
pic <- pic_normalizada * pca_result$scale + pca_result$center
pic [pic < 0] <- 0
pic [pic > 1] <- 1
pic
}
orig_pic <- train_matrix [100, ]
#orig pic <- test_matrix [300, ]
number_of_pca_components <- 400
t_pice <- transform_pca (row = orig_pic)
t_pic [number_of_pca_components: length (t_pic)] <- 0
dim (t_pic)
pic <- inv_transform_pca (row = t_pic)
plot_row_image (pic)
plot_row_image (orig_pic)

Ahora que hemos visto qué son los autovectores, cómo funcionan y cuál es la importancia de los componentes en estos, podemos pasar al siguiente nivel. Para ello, te ofrecemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, donde podrás formarte a nivel teórico y práctico en todo lo que necesitas para convertirte en un experto del sector IT. ¡Anímate y solicita más información para continuar forjando tu futuro!











