Los vectores en álgebra lineal son una especie de segmentos de líneas dirigidas que tienen una magnitud y una dirección. La longitud representa la magnitud y la orientación representa la dirección.
No obstante, la definición de vectores va a variar dependiendo del área en la que se trabaje. Si le preguntamos a un físico, nos va a decir que un vector es un array que tiene una longitud, una dirección y un sentido. Si le preguntamos a un software engineer, a alguien que trabaja constantemente con vectores, pero en un ambiente de programación, este nos va a dar una definición de vector como una lista de números.
Desde la perspectiva matemática, los vectores en álgebra son ambas cosas o, más bien, una mezcla de las dos.
Definición de los vectores
Se denomina vector de dimensión n a una tupla de números reales (que se llaman componentes del vector). Así, un vector perteneciente a un espacio Rn se representa como:
v = (a1, a2, a3, … an) donde v ∈ Rn
Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional R3 o bidimensional R2).
Tenemos, entonces, un eje de coordenadas que se compone de los ejes x e y. Tenemos dentro del eje una flecha que simula el vector A. Este vector tiene un origen, un final y una longitud.
Si el inicio es el punto A y el final es el punto B, entonces denominábamos al vector como:

Esta definición estaría muy bien si solo estuviéramos hablando de problemas del área de la física, pero ahora veremos un ejemplo en donde esta definición se queda corta.
Vamos a dibujar un vector en una recta que vaya de A a B del siguiente modo: el vector a viene definido por los componentes de g (x) y por los componentes de g (y). G (x) sería 3 y g (y) sería 2:
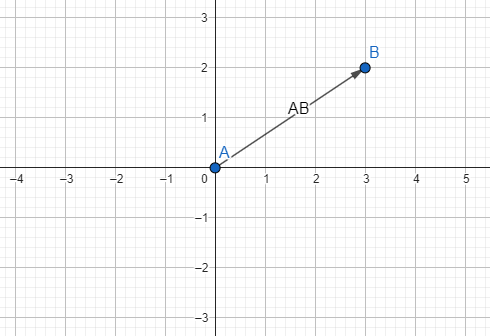
A = 3 / 2
En el área de software engineer con lo que se debe trabajar es con listas. Esa lista de números puede tener la cantidad de elementos que se prefiera o requiera.
Notación de vectores geométricos
Considerando el siguiente vector de O a A, contenido en el espacio bidimensional R2:
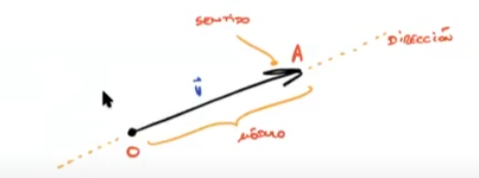
La posición del vector puede representarse como OA o v.
El módulo puede denotarse como: lOAl o OA o lvl. Está representado por el tamaño del vector, y hace referencia a la intensidad de la magnitud (número).
La dirección corresponde a la inclinación de la recta y representa al ángulo entre ella y un eje horizontal imaginario. El sentido está indicado por la punta de la flecha (signo positivo que, por lo general, no se coloca, o un signo negativo).
¿Qué podemos representar con un vector?
Considerando que un vector es una tupla de números reales, podemos usarlo para representar:
- Cadenas binarias: la clave secreta de un criptosistema 101101011 puede representarse como:
[1, 0, 1, 1, 0, 1, 0, 1, 1]
- Palabras: usando ciertos algoritmos (word2vec, glove…), podemos codificar las palabras a vectores únicos que representan dicha palabra.
king = [0.50451, 0.68607 -0.59517 -0.022801, 0.60046 -0.13498, -0.08813, 0.47 377 -0.61798, -0.310120.78321 -0.91241-1-6106 -0.64426, -0.51042]
- Distribuciones de probabilidad: la probabilidad de un dado.
[1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6, 1 / 6]
Vectores en Python
Para crear un vector en Python usamos la función array () de la biblioteca numpy.
#vectores en Python
import numpy as np
ex = np.array ([2, 3, 4, 5, 6, 7])
print (ex)[2 3 4 5 6 7]
print (type (ex))<class ‘numpy.ndarray’>
print (type ([2, 3, 4, 5, 6, 7]))
<class list»>
#vectores en Python
a = [2, 5]
b = [4, 5]
a + b[2, 5, 4, 5]
#vectores en Python
np.array ([2, 5]) + np.array ([4, 5])array ([6, 10])
Visualización de vectores con Python
Python es tremendamente potente para una infinidad de cosas. Una de las funciones más destacadas tiene que ver con la representación gráfica de información, la visualización de datos y todo lo relacionado con el mundo del Big Data. De ahí que Python tenga una amplia gama de opciones para casos de uso distintos.
En este caso, para la visualización de vectores con Python, vamos a utilizar la librería matplotlib y el comando interno @matplotlib inline para que nos muestre los datos en el notebook de jupyter dentro del que estamos trabajando.
En concreto, de matplotlib usaremos la función quiver, que nos proporciona esta librería para visualizar vectores. Lo único que haremos es definir el punto de inicio de los vectores y su dirección.
Quiver funciona, pero como veremos más adelante, no lo hace de manera muy óptima, ya que presenta algunos vacíos. Lo que sucede es que con esta opción puede llegar a ser un poco complejo configurar el gráfico a nuestro gusto.
Veamos un ejercicio de visualización de vectores con Python para entender mejor cómo trabajan y qué funcionalidades tiene este lenguaje.
Ejercicio de visualización de vectores con Python
Lo que haremos en primera instancia para la visualización de vectores con Python es importar las librerías necesarias, en este caso matplotlib y numpy. Acto seguido definiremos unos vectores, donde tenemos el componente x y el componente y.
#Ejercicio de visualización de vectores con matplotlib en Python
import matplotlib.pyplot as plt
import numpy as np
x_1 = 1
y_1 = 0
ux_1 = 0
uy_1 = 1
x_2 = 1.5
y_2 = 0
ux_2 = 0
uy_2 = -1
ax = plt.subplot ()
ax.quiver (x_1, y_1, ux_1, uy_1, angles = 'xy')
ax.quiver (x_2, y_2, ux_2, uy_2, angles = 'xy')
plt.show ()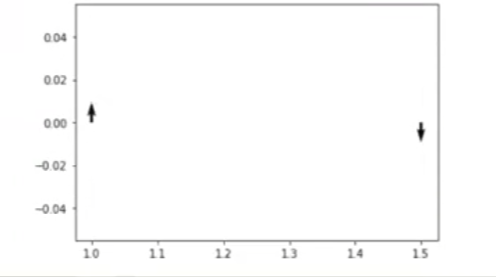
¿Qué hemos hecho aquí? En nuestro ejercicio de visualización de vectores con Python hemos definido dos vectores, el 1 y el 2. El vector 1 está definido en el 1 – 0, es decir, componente x igual a 1 y componente y igual a 0. La dirección del vector es hacia arriba, por eso tenemos en ux_1 un 0 y en uy_1 un 1.
En el caso del segundo vector tenemos que el eje x del mismo tiene un valor definido de 1.5 y en el eje y tiene un valor de 0. La dirección de este vector es negativa, lo que significa que va hacia abajo.
Lo que haremos después es poner el componente x y el componente y del primer vector (ax.quiver (x_1, y_1,…), luego proseguiremos con la dirección del primer vector en el eje x y la dirección del primer vector en el eje y (ux_2, uy_2). Por último, le tenemos que decir que siga unos ángulos específicos (angles = ‘xy’).
Después, hacemos exactamente el mismo proceso con el vector 2 y, con esto, ya lo tendríamos todo. ¡Solo queda mostrarlo!
El problema es un poco complicado graficarlo usando esta función. Si, por ejemplo, tenemos que representar tres vectores o más sobre el mismo punto, en el mismo origen, estos automáticamente se desplazan del origen y se torna un poco extraño y confuso de entender, además de la poca precisión que suponen estos cambios.
Quiver de matplotlib
Quiver es un tipo de diagrama en dos dimensiones que nos muestra líneas de vectores como flechas. Este tipo de diagrama es bastante útil cuando se requieren magnitud y dirección y se usa mucho en campos como la ingeniería eléctrica y electrónica para visualizar la intensidad de un campo eléctrico en cualquier dirección. También se emplea para visualizar el potencial eléctrico en ingeniería eléctrica.
¿Quieres seguir aprendiendo sobre Big Data?
Los vectores son una de las bases importantes en álgebra que debes aprender para comprender el Big Data. Esta área es una de las más demandadas a nivel laboral y, si te gustaría acceder a todas esas ofertas de empleo, tu mejor opción es formarte con el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con la guía de profesionales en el sector, adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños en menos de un año. ¡No esperes más para seguir tu camino hacia el éxito y solicita información ahora!



