¿Qué son los multiplicadores de Lagrange?

Los multiplicadores de Lagrange o método de Lagrange, los cuales deben su nombre a Joseph-Louis Lagrange, son una técnica que permite encontrar el máximo o mínimo de una función de varias dimensiones cuando hay alguna restricción en los valores de entrada que puede usar. Sigue leyendo y aprende sobre los multiplicadores de lagrange.

¿En qué consisten los multiplicadores de Lagrange?

En matemáticas, existe un concepto denominado programación no lineal (PNL), contraria a la PL, que es el proceso de resolución de un sistema de igualdades y desigualdades sujetas a un conjunto de restricciones sobre un conjunto de variables reales desconocidas. Tiene una función objetivo a maximizar (o minimizar) cuando alguna de las restricciones la función objetivo no son lineales.

El método de los multiplicadores de Lagrange o método de Lagrange nos permite encontrar los máximos y mínimos de una función multivariable cuando hay alguna restricción en los valores de entrada que puede usar.

La función de Lagrange, funcion lagrangiana o los multiplicadores de Lagrange, por tanto, ayuda a resolver problemas de optimización, ya que permite encontrar los máximos y los mínimos a partir de unas condiciones necesarias y unas condiciones suficientes para trabajar con múltiples variables.

Esta técnica de método de Lagrange solo se aplica a las restricciones de igualdad del tipo: g(x. y…) = c

Veamos dos ejemplos de multiplicadores de Lagrange

Calcular el mínimo de: f(x, y) = x² + y + 3

Condicionado a: g(x, y) = x + y = 5

// condiciones de primer orden lagrange
In [108]: f <- function(x,y){
                      x^2 + y + 3
}
g <- function(x, y){
        x + y 
}
const <- 5

Nuestra condición de los multiplicadores de Lagrange se puede escribir como:

g(x , y) = x+ y =5

y = 5 – x

// ecuación de lagrange
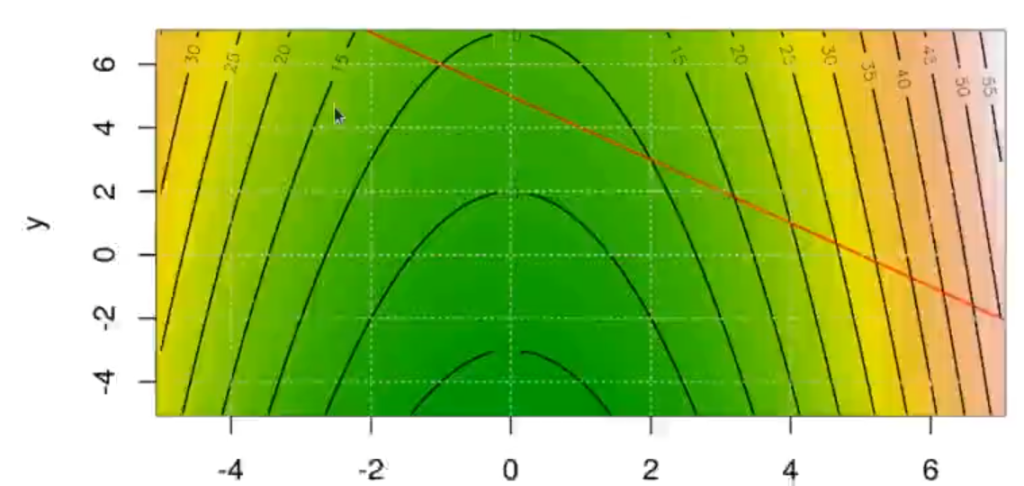
In (114): plotMyFunc (f, c (-5, 7))
ablinet (c (const, -1), col = "red")
grid()

La gráfica de los multiplicadores de Lagrange quedaría más o menos así:

In [115]: f_inv <- function (f, x) {
                      y <- f - x^2 - 3
                      return (y)
}
g: inv <- function(g, x) {
               g-x
}

In [116]: x-seq(-2, 5, length.out = 100)
y <- g_inv(const, x)

In [123]: yf <- f_inv(7.75, x)

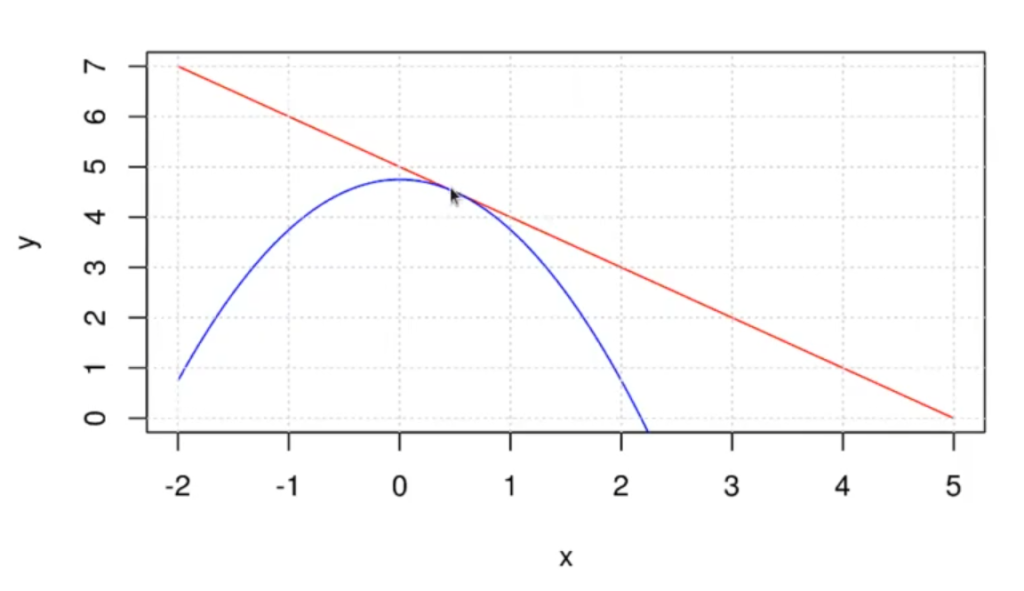
plot(x, y, t = 'l', col = "red")
lines(x, yf, t = 'l', col = "blue")
grid()

La gráfica de los multiplicadores de Lagrange quedaría así:

Los multiplicadores de Lagrange pueden ser muy útiles cuando trabajamos con variables múltiples, pero también variables únicas. Son también necesarios para optimizar muchos de los procesos llevados a cabo en el Big data.

Si quieres seguir aprendiendo acerca de estos temas, recuerda que tenemos disponible para ti nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en el que aprenderás todo lo necesario para incursionar en el mercado laboral y convertirte en un profesional en tan solo 8 meses. ¡Anímate a pedir información y forja tu futuro en el sector IT!