¿Qué son las redes neuronales matemáticas? Entiéndelas con ejemplos

Las redes neuronales matemáticas imitan el funcionamiento del cerebro humano utilizando funciones matemáticas.

De hecho, han logrado cambiar la forma en que abordamos problemas complejos y se usan tanto en la inteligencia artificial como en la matemática aplicada.

En este artículo, desglosaremos qué son exactamente las redes neuronales matemáticas, cómo funcionan y te daremos algunos ejemplos prácticos para que las entiendas mejor.

¿Qué son las redes neuronales matemáticas?

Las redes neuronales matemáticas son modelos computacionales inspirados en el funcionamiento del cerebro humano.

Estas redes están compuestas por capas de «neuronas» artificiales que procesan información de manera similar a como lo hace el cerebro.

En lugar de trabajar con conexiones biológicas, estas neuronas artificiales están conectadas mediante funciones matemáticas que ayudan a resolver problemas como la clasificación, el reconocimiento de patrones o la predicción de datos.

• Imagina que las redes neuronales son como un equipo de trabajadores, donde cada uno tiene una pequeña tarea específica. Juntos, colaboran para resolver un problema grande y complejo.

Así es como funcionan las redes neuronales matemáticas: dividen el trabajo en pequeñas partes y combinan los resultados para obtener una solución.

La estructura matemática de una red neuronal

Una red neuronal se organiza en varias capas: capa de entrada, capas ocultas y capa de salida.

Cada neurona dentro de una capa se conecta a las neuronas de la siguiente capa mediante pesos.

Estos pesos determinan la influencia que una neurona tiene sobre otra, y son fundamentales para que la red «aprenda».

El proceso matemático dentro de una neurona se basa en la siguiente fórmula:

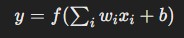
Donde:

• wi son los pesos,
• xi son los valores de entrada,
• b es el sesgo (bias),
• f es la función de activación, que introduce no linealidad al modelo.

¿Cómo aprenden las redes neuronales matemáticas?

El aprendizaje en las redes neuronales matemáticas se realiza mediante un proceso llamado propagación hacia atrás (backpropagation).

En este proceso, la red ajusta los pesos y los sesgos para minimizar el error entre la salida predicha y el resultado real.

Piensa en ello como un sistema de prueba y error, donde la red corrige sus errores gradualmente hasta que aprende a realizar predicciones precisas.

Este aprendizaje ocurre en dos fases:

1. Propagación hacia adelante: La información pasa a través de las capas y produce un resultado.
2. Retropropagación: El error entre el resultado predicho y el real se retroalimenta para ajustar los pesos.

Ejemplo de una red neuronal simple

Supongamos que queremos predecir si un día será soleado o lluvioso basándonos en dos entradas: temperatura y humedad.

Cada entrada se multiplica por un peso y luego se suma con un sesgo. Finalmente, una función de activación decide si la salida será «soleado» o «lluvioso».

En este caso, la red neuronal procesa las entradas y ajusta los pesos mediante el aprendizaje, mejorando sus predicciones a medida que recibe más ejemplos.

Aplicaciones de las redes neuronales matemáticas

Las redes neuronales tienen una amplia gama de aplicaciones en el mundo real. Algunos ejemplos incluyen:

• Reconocimiento de voz: En asistentes virtuales como Siri o Google Assistant.
• Reconocimiento de imágenes: En sistemas de seguridad que identifican rostros.
• Predicción financiera: En algoritmos de trading que predicen el comportamiento del mercado.

¿Cómo se usan las redes neuronales en machine learning?

En machine learning, las redes neuronales se utilizan para crear modelos que pueden aprender de los datos sin ser programados explícitamente para resolver un problema específico.

A través del entrenamiento con grandes conjuntos de datos, estas redes aprenden a identificar patrones y realizar predicciones precisas.

• Por ejemplo, en el reconocimiento de imágenes, una red neuronal puede aprender a distinguir entre un gato y un perro después de ser entrenada con miles de imágenes etiquetadas.

Ventajas y limitaciones de las redes neuronales matemáticas

Ventajas:

• Capacidad de aprendizaje: Pueden aprender de los datos y mejorar con el tiempo.
• Versatilidad: Se aplican en muchos campos, desde el procesamiento del lenguaje natural hasta la visión por computadora.

Limitaciones:

• Requieren grandes cantidades de datos: Para que funcionen correctamente, se necesita un volumen considerable de ejemplos de entrenamiento.
• Tiempo de entrenamiento: Pueden tardar mucho en entrenarse, especialmente si no se utilizan recursos computacionales avanzados.

¿Cómo puedes crear tu propia red neuronal?

Hoy en día, existen muchas herramientas que te permiten crear y entrenar tus propias redes neuronales sin tener que implementar todo desde cero.

Bibliotecas populares como TensorFlow y PyTorch ofrecen una manera sencilla de construir redes complejas y entrenarlas con grandes volúmenes de datos.

Un ejemplo básico en Python sería:

import tensorflow as tf
from tensorflow.keras import layers

# Crear un modelo secuencial
model = tf.keras.Sequential([
    layers.Dense(64, activation='relu', input_shape=(2,)),
    layers.Dense(1, activation='sigmoid')
])

# Compilar el modelo
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# Entrenar el modelo
model.fit(X_train, y_train, epochs=10)

Continúa con la creación de redes neuronales matemáticas en el Bootcamp de Big Data, Data Science, Machine Learning e IA de KeepCoding. ¡Anímate y aprende de la mano de expertos hoy mismo!