¿Sabes cómo funciona la regresión lineal con t-student y ANOVA?
Si has estudiado estadística en Big Data, sabrás que la regresión lineal con t-student y ANOVA es primordial para realizar análisis estadísticos y predictivos; por eso, en este post te explicaremos en qué consisten y cómo los puedes aplicar en regresión lineal.
¿Qué son t-student y ANOVA?
T-student
También llamadas T Distribution o Student’s T Distribution. Son un conjunto de distribuciones muy similares a la curva de distribución normal. Se usa como reemplazo de la distribución normal cuando se tienen muestras muy pequeñas. Cuanto mayor sea el tamaño de la muestra, más parecida será la distribución T a la distribución normal.
ANOVA
El análisis de varianza es una fórmula estadística utilizada para comparar varianzas entre medias de distintos conjuntos de datos. La prueba ANOVA se utiliza para determinar la influencia que tienen las variables independientes sobre la variable dependiente en un modelo o estudio de regresión lineal.
¿Qué relación tiene la regresión lineal con t-student y ANOVA?
La regresión lineal con t-student y ANOVA tiene una explicación simple. Como sabemos, los coeficientes tienen un error, un margen de confianza que viene de una varianza que estamos calculando en función del mismo error. La varianza nos ayuda a crear el test estadístico, que sigue una distribución t-student.
Suponiendo que los residuos siguen una distribución gaussiana, se puede calcular la varianza de cada uno de los coeficientes como:
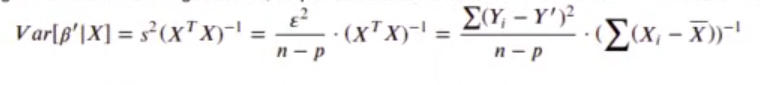
Donde:
- p es el número de grados de libertad, de coeficientes. En este caso son 2: intersección y la pendiente.
- n es el número de muestras.
La media de los coeficientes viene dada por el vector Bi. Con la media y la varianza podemos calcular la probabilidad de que el valor de la media estimada esté muy desviada de 0 por puro azar. Eso aparece con el valor Pr(>ltl) en el summary del modelo. Cuanto menos sea este valor, más fiable será. Más adelante veremos qué significa esta probabilidad en detalle, llamada p-valor.
Donde Pr(>ltl) vendrá a ser un test de dos hipótesis:
- H0: el valor del coeficiente no es importante para la regresión. Su valor debería ser 0.
- H1: el valor del coeficiente es importante para la regresión. Su valor debería ser diferente a 0.
¿Ahora te queda más claro cómo funciona eso de la regresión lineal con t-student y ANOVA? para seguir profundizando en este tema y mucho otros relacionados, puedes seguir nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, donde aprenderás en poco tiempo todo lo necesario para incursionar en el mercado laboral del Big Data. ¡No pierdas la oportunidad de pedir más información y descubre cómo cambiar tu vida!











